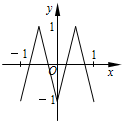题目内容
10.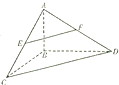 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点(1)判断直线EF与平面BCD的位置关系,并说明理由
(2)求三棱锥A-BCD的体积.
分析 (1)在△ACD中,点E,F分别是AC,AD的中点,由三角形中位线定理可得EF∥CD,然后利用线面平行的判定得答案;
(2)直接由三棱锥的体积公式结合已知条件求得三棱锥A-BCD的体积.
解答 解:(1)EF∥平面BCD. 事实上,
事实上,
∵在△ACD中,点E,F分别是AC,AD的中点,∴EF∥CD,
又∵EF?平面BCD,CD?平面BCD,
∴EF∥平面BCD;
(2)∵AB⊥平面BCD,∴AB为三棱锥A-BCD的高,
又BC⊥BD,BC=BD=4,∴${S}_{△BCD}=\frac{1}{2}×4×4=8$,
又AB=3,∴${V}_{A-BCD}=\frac{1}{3}×8×3=8$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
15.设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,-3,1)的距离相等,则点P的坐标是( )
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |
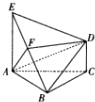 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.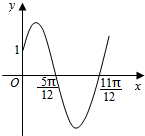 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.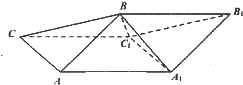 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
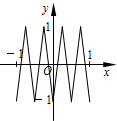
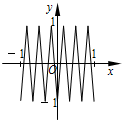
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.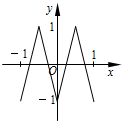 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )