题目内容
6.“$\frac{1}{a}$>1”是“函数f(x)=(3-2a)x单调递增”( )| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分且必要 | D. | 既不充分也不必要 |
分析 根据充分条件和必要条件的定义结合条件求出对应的等价条件,进行判断即可.
解答 解:由$\frac{1}{a}$>1得0<a<1,
若函数f(x)=(3-2a)x单调递增,
则3-2a>1,
解得a<1,
故“$\frac{1}{a}$>1”是“函数f(x)=(3-2a)x单调递增”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据不等式的关系以及指数函数的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如表是某厂1-4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有线性相关关系,其线性回归方程是$\widehat{y}$=-0.7x+$\widehat{a}$,则$\widehat{a}$=( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |
14.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
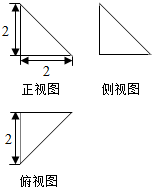

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
15.设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,-3,1)的距离相等,则点P的坐标是( )
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |
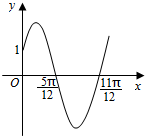 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.