题目内容
13.对任意给定的实常数a,设命题p:方程ax2+(a-2)y2=1的曲线是双曲线;命题q:?x0>0,x0+a-1=0,若“p∧(¬q)”为真命题,则a的取值范围是[1,2).分析 若p∧(¬q)为真,则p真,q假,然后分别求出p,q为真命题的等价条件即可.
解答 解:∵“p∧(¬q)”为真命题,
∴p真,q假,
若命题p为真,则a(a-2)<0,即0<a<2,
若命题¬q为真,?x>0,x+a-1≠0,则1-a≤0,即a≥1,
∴$\left\{\begin{array}{l}{0<a<2}\\{a≥1}\end{array}\right.$,
解得1≤a<2
故a的取值范围为[1,2).
故答案为:[1,2).
点评 本题主要考查复合命题的应用,要求熟练掌握复合命题与简单命题的真假关系.

练习册系列答案
相关题目
3. 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )| A. | 甲 | B. | 乙 | C. | 甲、乙相等 | D. | 无法确定 |
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |
8.口袋里装有大小相同的3个白球和2个黑球,每次从中不放回随机抽取1个球,连续抽出2次,则在第一次抽到白球的条件下,第二次抽到白球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
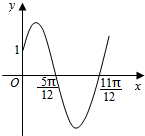 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.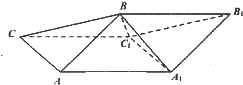 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.