题目内容

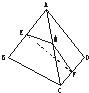
在三棱锥A-BCD中，AD=BC=2a，E、F分别是AB、CD的中点，EF=
3
a，求AD与BC所成的角．
取AC的中点M，连接ME、MF，则ME∥BC，MF∥AD，所以∠EMF（或其补角）是直线AD与BC所成的角．
∵在△EMF中，ME=
1
2
BC=a，MF=
1
2
AD=a，EF=
3
a，
∴cos∠EMF=
a2+a2-3a2
2a2
=-
1
2
，
∴∠EMF=120°，
因此异面直线AD与BC所成的角为60°．
练习册系列答案
相关题目
（理）如图，已知正三棱柱ABC-A1B1C1的各条棱长都相等，M是侧棱CC1的中点，则异面直线AB1和BM所成的角的大小是（　　）
A．90°B．60°C．45°D．30°
如图：四面体P-ABC为正四面体，M为PC的中点，则BM与AC所成的角的余弦值为______．
如图所示，正方体ABCD-A1B1C1D1中，AA1=2，E为棱CC1上的点，则B1D1与AE所成的角（　　）
A．30°B．45°C．60°D．90°
如图ABCD-A1B1C1D1是正方体，B1E1=D1F1=
A1B1
4
，则BE1与DF1所成的角的余弦值是（　　）
A．
15
17
B．
1
2
C．
8
17
D．
3
2
在棱长为1的正方体ABCD-A1B1C1D1中，M和N分别为A1B1和BB1的中点，那么直线AM与CN所成角的余弦值是（　　）
A．
3
2
B．
10
10
C．
3
5
D．
2
5
在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，若AC=BD=a，且AC与BD所成的角为45°，则四边形EFGH的面积为（　　）
A．
2
16
a2		B．
2
8
a2		C．
2
4
a2		D．
2
2
a2
在正四面体ABCD中，点E、F分别为BC、AD的中点，则AE与CF所成角的余弦值为（　　）
A．-
2
3
B．
2
3
C．-
1
3
D．
1
3
如图，正方体ABCD-A1B1C1D1中E为AB的中点．
（1）求直线A1C1与平面A1B1CD所成角大小；
（2）试确定直线BC1与平面EB1D的位置关系，并证明你的结论；
（3）证明：平面EB1D⊥平面B1CD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网