Question

如图：四面体P-ABC为正四面体，M为PC的中点，则BM与AC所成的角的余弦值为______．

Answer 1

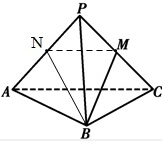
取AP的中点N，连结MN、BN，可得
∵△PAC中，MN是中位线，
∴MN∥AC且MN=

1

2

AC．
因此∠NMB（或其补角）就是BM与AC所成的角．
设正四面体P-ABC的棱长为2，
则△BMN中，MN=

1

2

AC=1，BN=BM=

3

，
∴由余弦定理，可得cos∠NMB=

1+3-3

2×1× 3

=

3

6

，
由此可得BM与AC所成的角的余弦值为

3

6

故答案为：

3

6