题目内容

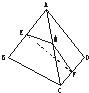
在正四面体ABCD中，点E、F分别为BC、AD的中点，则AE与CF所成角的余弦值为（　　）
A．-
2
3
B．
2
3
C．-
1
3
D．
1
3
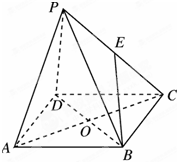
如图所示，作AO⊥底面BCD，垂足为O，O为底面等边△BCD的中心，建立空间直角坐标系．
不妨取CD=2．则C（1，
3
3
，0），D(-1，
3
3
，0)，B(0，-
2
3
3
，0)，
E(
1
2
，-
3
6
，0)，
设点M是线段CD的中点，则AM=
3
，OM=
1
3
，BM=
3
3
．
∴AO=
(AM)2-(OM)2
=
(
3
)2-(
3
3
)2
=
2
6
3
．
∴A(0，0，
2
6
3
)．
∴F(-
1
2
，
3
6
，
6
3
)，
∴
AE
=(
1
2
，-
3
6
，-
2
6
3
)，
CF
=(-
3
2
，-
3
6
，
6
3
)．
∴cos＜
AE
，
CF
＞=
AE
•
CF
|
AE
||
CF
|
=
-
3
4
+
1
12
-
4
3
3
×
3
=-
2
3
．
∴异面直线AE与CF所成角的余弦值为
2
3
．
故选：B．
练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中，O为AC，BD的交点，则C1O与A1D所成角余弦（　　）
A．
1
2
B．0C．
3
6
D．
3
3
在三棱锥A-BCD中，AD=BC=2a，E、F分别是AB、CD的中点，EF=
3
a，求AD与BC所成的角．
正四棱锥P-ABCD的底面积为3，体积为
2
2
，E为侧棱PC的中点，则PA与BE所成的角为（　　）
A．
π
6
B．
π
3
C．
π
4
D．
π
2
在四棱锥P-ABCD中，底面ABCD是一直角梯，∠BAD=90°，AD∥BC，AB=BC=a，AD=2a，PA⊥底面ABCD，PD与底面成30°角．
（1）若AE⊥PD，E为垂足，求证：BE⊥PD；
（2）在（1）的条件下，求异面直线AE与CD所成角的余弦值；
（3）求平面PAB与平面PCD所成的锐二面角的正切值．
已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．

（1）求证：BN⊥平面C1B1N；
（2）设θ为直线C1N与平面CNB1所成的角，求sinθ的值；
（3）设M为AB中点，在BC边上求一点P，使MP∥平面CNB1，求
BP
PC
的值．
如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是矩形，且SD=AD=
2
AB，E是SA的中点．
（1）求证：平面BED⊥平面SAB；
（2）求直线SA与平面BED所成角的大小．
正方体ABCD-A1B1C1D1中，对角线AC1与底面ABCD所成角的正切值等于（　　）
A．1B．
2
C．
2
2
D．
3
3
在直三棱柱ABC-A1B1C1中，CA=CB=CC1=2，∠ACB=90°，E、F分别是BA、BC的中点，G是AA1上一点，且AC1⊥EG．
（Ⅰ）确定点G的位置；
（Ⅱ）求直线AC1与平面EFG所成角θ的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网