题目内容
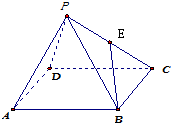
如图所示,正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1上的点,则B1D1与AE所成的角( )
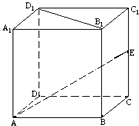
| A.30° | B.45° | C.60° | D.90° |

根据正方体的几何特征,我可得:
B1D1⊥AC,且B1D1⊥EC
又由AC∩EC=C
∴B1D1⊥平面ACE
又由AE?平面ACE
∴B1D1⊥AE
即B1D1与AE所成的角为90°
故选D.
B1D1⊥AC,且B1D1⊥EC
又由AC∩EC=C
∴B1D1⊥平面ACE
又由AE?平面ACE
∴B1D1⊥AE
即B1D1与AE所成的角为90°
故选D.

练习册系列答案
相关题目
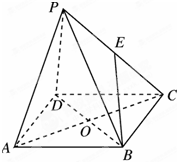
 分)如图,五面体
分)如图,五面体
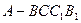 中
中
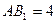 .底面
.底面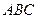 是正三角形,
是正三角形,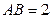 .
. 四边形
四边形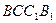 是矩形
是矩形 ,
, 二面角
二面角
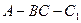 为直二面角.
为直二面角.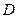 在
在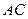 上运动,当
上运动,当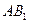 ∥平面
∥平面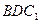 ,并且
,并且 说明理由;
说明理由;
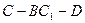
 的
的 余弦值.
余弦值.