题目内容
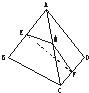
在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,若AC=BD=a,且AC与BD所成的角为45°,则四边形EFGH的面积为( )
A.
| B.
| C.
| D.
|
因为EH是△ABD的中位线,所以EH∥BD,且2EH=BD=a.
同理,FG∥BD,EF∥AC,且2FG=BD,2EF=AC=a.
所以EH∥FG,且EH=FG.且∠FEH为异面直线AC与BD所成的角,
所以四边形EFGH为平行四边形.
因为AC=BD,
所以EF=EH=
.
所以四边形EFGH为菱形.
∵AC与BD所成的角为45°,
∴∠FEH=45°或135°,
∴S=
×
×sin45°=
a2.
故选B.

同理,FG∥BD,EF∥AC,且2FG=BD,2EF=AC=a.
所以EH∥FG,且EH=FG.且∠FEH为异面直线AC与BD所成的角,
所以四边形EFGH为平行四边形.
因为AC=BD,
所以EF=EH=
| a |
| 2 |
所以四边形EFGH为菱形.
∵AC与BD所成的角为45°,
∴∠FEH=45°或135°,
∴S=
| a |
| 2 |
| a |
| 2 |
| ||
| 8 |
故选B.


练习册系列答案
相关题目