题目内容
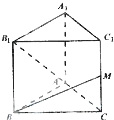
(理)如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
| A.90° | B.60° | C.45° | D.30° |

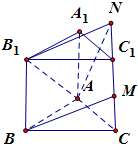
设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN,则
∵MN∥BB1,MN=BB1,∴四边形BB1NM是平行四边形,可得B1N∥BM
因此,∠AB1N(或其补角)就是异面直线AB1和BM所成角
∵Rt△B1C1N中,B1C1=2,C1N=1,∴B1N=
∵Rt△ACN中,AC=2,CN=3,∴AN=
又∵正方形AA1B1B中,AB1=2
∴△AB1N中,cos∠AB1N=
=0,可得∠AB1N=90°
即异面直线AB1和BM所成角为90°
故选:A
∵MN∥BB1,MN=BB1,∴四边形BB1NM是平行四边形,可得B1N∥BM
因此,∠AB1N(或其补角)就是异面直线AB1和BM所成角
∵Rt△B1C1N中,B1C1=2,C1N=1,∴B1N=
| 5 |
∵Rt△ACN中,AC=2,CN=3,∴AN=
| 13 |
又∵正方形AA1B1B中,AB1=2
| 2 |
∴△AB1N中,cos∠AB1N=
| 5+8-13 | ||||
2×
|
即异面直线AB1和BM所成角为90°
故选:A


练习册系列答案
相关题目
 在平面
在平面 上的射影为正
上的射影为正 ,若
,若 ,
, ,
, ,求平面
,求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.

 分)如图,五面体
分)如图,五面体
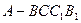 中
中
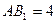 .底面
.底面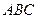 是正三角形,
是正三角形,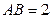 .
. 四边形
四边形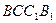 是矩形
是矩形 ,
, 二面角
二面角
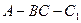 为直二面角.
为直二面角.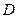 在
在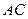 上运动,当
上运动,当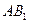 ∥平面
∥平面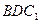 ,并且
,并且 说明理由;
说明理由;
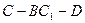
 的
的 余弦值.
余弦值.