题目内容
17.已知函数f(x)=x2-(a+1)x+1(a∈R).(1)若关于x的不等式f(x)≥0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)<0的解集是{x|b<x<2},求a,b的值;
(3)若关于x的不等式f(x)≤0的解集是 P,集合Q={x|0≤x≤1},若 P∩Q=∅,求实数a的取值范围.
分析 (1)应用一元二次不等式恒成立时判别式△≤0,求出a的取值范围;
(2)根据一元二次不等式与对应一元二次方程的关系,列出方程组,求出a、b的值;
(3)问题转化为不等式f(x)>0对x∈Q恒成立,由此求出a的取值范围.
解答 解:(1)∵f(x)=x2-(a+1)x+1(a∈R),
且关于x的不等式f(x)≥0的解集为R,
∴△=(a+1)2-4≤0,
解得-3≤a≤1,
∴实数a的取值范围是-3≤a≤1;
(2)∵关于x的不等式f(x)<0的解集是{x|b<x<2},
∴对应方程x2-(a+1)x+1=0的两个实数根为b、2,
由根与系数的关系,得$\left\{\begin{array}{l}{b•2=1}\\{b+2=a+1}\end{array}\right.$,
解得a=$\frac{3}{2}$,b=$\frac{1}{2}$;
(3)∵关于x的不等式f(x)≤0的解集是 P,
集合Q={x|0≤x≤1},当 P∩Q=∅时,
即不等式f(x)>0对x∈Q恒成立;
∴x∈[0,1]时,x2-(a+1)x+1>0恒成立,
∴a+1<x+$\frac{1}{x}$对于x∈(0,1]时恒成立;
∴a+1<2,
即a<1,
∴实数a的取值范围是a<1.
点评 本题考查了二次函数与一元二次方程以及对应不等式的解法与应用问题,考查了转化思想的应用问题,是综合性题目.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
8.运行如图所示的程序框图,若输出的结果是36,则输入的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
12.四边形ABCD中,AB=BC,AD⊥DC,AC=1,∠ACD=θ,若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$,则cos2θ等于( )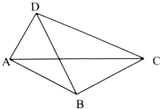

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
2.椭圆C:$\frac{x^2}{16}+\frac{y^2}{9}$=1的左、右顶点分别为A1,A2,点P是C上异于顶点的任一点,则直线PA2与直线PA1的斜率之积是( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{9}{16}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{16}{9}$ |
4.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算K2≈0.99,根据这一数据分析,下列说法正确的是( )
| A. | 有99%的人认为该栏目优秀 | |
| B. | 有99%的人认为该栏目是否优秀与改革有关系 | |
| C. | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D. | 没有理由认为电视栏目是否优秀与改革有关系 |
1.函数y=$\frac{3{x}^{2}}{\sqrt{1-2x}}$+(2x+1)2的定义域为( )
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<$\frac{1}{2}$且x≠-$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|x≤$\frac{1}{2}$且x≠-$\frac{1}{2}$} |
2.命题“?x0∈(0,+∞),2x0<x02”的否定为( )
| A. | ?x∈(0,+∞),2x<x2 | B. | ?x∈(0,+∞),2x>x2 | C. | ?x∈(0,+∞),2x≥x2 | D. | ?x∈(0,+∞),2x≥x2 |
 过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.
过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.