为了评价某个电视栏目的改革效果.在改革前后分别从居民点抽取了100位居民进行调查.经过计算K2≈0.99.根据这一数据分析.下列说法正确的是( )A．有99%的人认为该栏目优秀B．有99%的人认为该栏目是否优秀与改革有关系C．有99%的把握认为电视栏目是否优秀与改革有关系D．没有理由认为电视栏目是否优秀与改革有关系题目和参考答案——青夏教育精英家教网—

题目内容

4．为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算K²≈0.99，根据这一数据分析，下列说法正确的是（　　）

	A．	有99%的人认为该栏目优秀
	B．	有99%的人认为该栏目是否优秀与改革有关系
	C．	有99%的把握认为电视栏目是否优秀与改革有关系
	D．	没有理由认为电视栏目是否优秀与改革有关系

分析根据k²的参考表，进行判断即可．

解答解：

P（K²＞k）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

只有K²＞0.708，
所以可以说在犯错率不超过0.4的条件下认为该栏目是否优秀与改革有关系，即有60%的把握认为电视栏目是否优秀与改革有关系，
故没有理由认为电视栏目是否优秀与改革有关系，
故选D．

点评本题的考查点是独立性检验的应用，根据独立性检测考查两个变量是否有关系的方法进行判断，准确的理解判断方法及K²的含义是解决本题的关键．

练习册系列答案

20．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的函数是（　　）

y=2^x+log₂x

$y={x^{\frac{1}{2}}}$

17．已知函数f（x）=x²-（a+1）x+1（a∈R）．
（1）若关于x的不等式f（x）≥0的解集为R，求实数a的取值范围；
（2）若关于x的不等式f（x）＜0的解集是{x|b＜x＜2}，求a，b的值；
（3）若关于x的不等式f（x）≤0的解集是 P，集合Q={x|0≤x≤1}，若 P∩Q=∅，求实数a的取值范围．

4．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁、F₂．
（1）若点A（0，b）与焦点F₁、F₂构成△AF₁F₂为等腰直角三角形，求椭圆的离心率．
（2）若椭圆E的离心率为$\frac{1}{2}$，过点P（0，1）的直线与椭圆交于B、C两点，且当点B、C关于y轴对称时，|BC|=$\frac{{4\sqrt{6}}}{3}$，求椭圆E的方程．

9．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁，F₂，过点（1，$\frac{{\sqrt{2}}}{2}$），离心率e=$\frac{{\sqrt{2}}}{2}$．
（1）求椭圆的标准方程；
（2）过点F₁的直线l与该椭圆交于M，N两点，且|${\overrightarrow{{F_2}M}$+$\overrightarrow{{F_2}N}}$|=$\frac{{2\sqrt{26}}}{3}$，求直线l的方程．

16．已知椭圆C的中心在原点，左焦点F₁，右焦点F₂均在x轴上，A为椭圆的右顶点，B为椭圆短轴的端点，P是椭圆上一点，且PF₁⊥x轴，PF₂∥AB，则此椭圆的离心率等于（　　）

A．

$\frac{1}{2}$

B．

$\frac{{\sqrt{2}}}{2}$

C．

$\frac{1}{3}$

D．

$\frac{{\sqrt{5}}}{5}$

13．

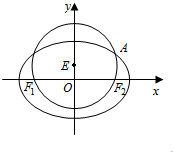已知圆E：x²+（y-$\frac{1}{2}$）²=$\frac{9}{4}$经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点F₁，F₂，且与椭圆C在第一象限的交点为A，且F₁，E，A三点共线，直线l交椭圆C于M，N两点，且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$（λ≠0）
（1）求椭圆C的方程；
（2）当三角形AMN的面积取得最大值时，求直线l的方程．

14．已知复数w满足w-4=（3-2w）i（i为虚数单位），$z=\frac{5}{w}+|\overline w-2|$．
（1）求z；
（2）若（1）中的z是关于x的方程x²-px+q=0的一个根，求实数p，q的值及方程的另一个根．

试题分类