题目内容
12.四边形ABCD中,AB=BC,AD⊥DC,AC=1,∠ACD=θ,若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$,则cos2θ等于( )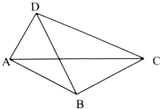
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 如图所示,取AC的中点O,连接OD,OB.由AB=BC,OA=OC,可得OB⊥AC.于是$\overrightarrow{OB}•\overrightarrow{AC}$=0.又$\overrightarrow{DB}=\overrightarrow{DO}+\overrightarrow{OB}$,$\overrightarrow{DO}$=$\frac{1}{2}(\overrightarrow{DA}+\overrightarrow{DC})$,代入可得$\frac{1}{3}$=$\overrightarrow{DB}•\overrightarrow{AC}$=$\frac{1}{2}({\overrightarrow{DC}}^{2}-{\overrightarrow{DA}}^{2})$,设$|\overrightarrow{DC}|$=m,$|\overrightarrow{DA}|$=n.
则m2-n2=$\frac{2}{3}$.又m2+n2=AC2=1,联立解得m,n.可得cosθ.利用cos2θ=2cos2θ-1即可得出.
解答 解:如图所示,取AC的中点O,连接OD,OB.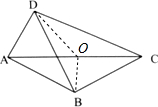
∵AB=BC,OA=OC,
∴OB⊥AC.
∴$\overrightarrow{OB}•\overrightarrow{AC}$=0.
∵$\overrightarrow{DB}=\overrightarrow{DO}+\overrightarrow{OB}$,$\overrightarrow{DO}$=$\frac{1}{2}(\overrightarrow{DA}+\overrightarrow{DC})$,
∴$\frac{1}{3}$=$\overrightarrow{DB}•\overrightarrow{AC}$=$(\overrightarrow{DO}+\overrightarrow{OB})$$•\overrightarrow{AC}$=$\overrightarrow{DO}•\overrightarrow{AC}$=$\frac{1}{2}(\overrightarrow{DA}+\overrightarrow{DC})$$•(\overrightarrow{DC}-\overrightarrow{DA})$=$\frac{1}{2}({\overrightarrow{DC}}^{2}-{\overrightarrow{DA}}^{2})$,
设$|\overrightarrow{DC}|$=m,$|\overrightarrow{DA}|$=n.
则m2-n2=$\frac{2}{3}$.
又∵AD⊥DC,∴m2+n2=AC2=1,
联立解得m=$\frac{\sqrt{30}}{6}$,n=$\frac{\sqrt{6}}{6}$.
∴$cosθ=\frac{DC}{AC}$=$\frac{\sqrt{30}}{6}$.
∴cos2θ=2cos2θ-1=2×$(\frac{\sqrt{30}}{6})^{2}$-1=$\frac{2}{3}$,
故选:D.
点评 本题考查了向量的平行四边形法则、数量积运算性质、等腰三角形的性质、勾股定理、倍角公式,考查了推理能力与计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1-i | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
| A. | y=x+x-1 | B. | y=x3+x | C. | y=2x+log2x | D. | $y={x^{\frac{1}{2}}}$ |
| A. | [-1,$\frac{1}{2}$) | B. | [-2,$\frac{1}{2}$) | C. | [-2,$\frac{3}{2}$) | D. | [-1,$\frac{3}{2}$) |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |