题目内容
数列{an}满足:a1=1,an+1=3an+2n+1(n∈N*),求{an}的通项公式.
an=5×3n-1-2n+1
两端同除以2n+1得,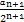 =
= ·
·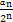 +1,
+1,
即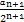 +2=
+2= (
(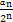 +2),
+2),
即数列{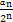 +2}是首项为
+2}是首项为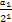 +2=
+2= ,公比为
,公比为 的等比数列,故
的等比数列,故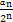 +2=
+2= ×(
×( )n-1,即an=5×3n-1-2n+1.
)n-1,即an=5×3n-1-2n+1.
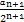 =
= ·
·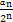 +1,
+1,即
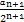 +2=
+2= (
(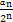 +2),
+2),即数列{
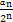 +2}是首项为
+2}是首项为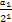 +2=
+2= ,公比为
,公比为 的等比数列,故
的等比数列,故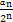 +2=
+2= ×(
×( )n-1,即an=5×3n-1-2n+1.
)n-1,即an=5×3n-1-2n+1.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
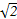

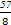
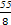
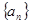 中,已知
中,已知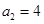 ,
,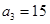 ,且数列
,且数列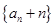 是等比数列,则
是等比数列,则 .
.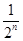 ,n∈N*,则:
,n∈N*,则: