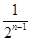题目内容
设Sn为数列{an}的前n项和,Sn=(-1)nan-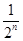 ,n∈N*,则:
,n∈N*,则:
(1)a3=________;
(2)S1+S2+…+S100=________.
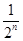 ,n∈N*,则:
,n∈N*,则:(1)a3=________;
(2)S1+S2+…+S100=________.
(1)-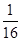 (2)
(2)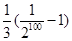
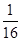 (2)
(2)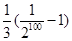
(1)∵Sn=(-1)nan-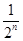 .
.
当n=3时,a1+a2+a3=-a3-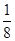 ,①
,①
当n=4时,a1+a2+a3+a4=a4-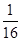 ,
,
∴a1+a2+a3=-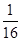 ,②由①②知a3=-
,②由①②知a3=-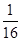 ,
,
(2)n>1时,Sn-1=(-1)n-1an-1-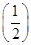 n-1,∴an=(-1)nan+(-1)nan-1+
n-1,∴an=(-1)nan+(-1)nan-1+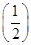 n.
n.
当n为奇数时,an=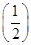 n+1-
n+1-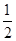 an-1;当n为偶数时,an-1=-
an-1;当n为偶数时,an-1=-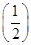 n.
n.
故an=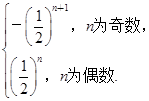 ∴Sn=
∴Sn=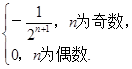
∴S1+S2+…+S100=-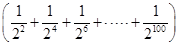 =-
=-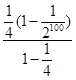 =-
=-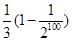 =
=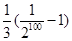 .
.
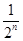 .
.当n=3时,a1+a2+a3=-a3-
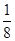 ,①
,①当n=4时,a1+a2+a3+a4=a4-
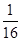 ,
,∴a1+a2+a3=-
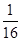 ,②由①②知a3=-
,②由①②知a3=-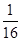 ,
,(2)n>1时,Sn-1=(-1)n-1an-1-
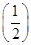 n-1,∴an=(-1)nan+(-1)nan-1+
n-1,∴an=(-1)nan+(-1)nan-1+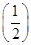 n.
n.当n为奇数时,an=
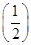 n+1-
n+1-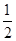 an-1;当n为偶数时,an-1=-
an-1;当n为偶数时,an-1=-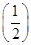 n.
n.故an=
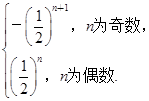 ∴Sn=
∴Sn=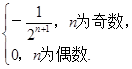
∴S1+S2+…+S100=-
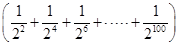 =-
=-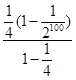 =-
=-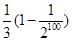 =
=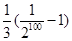 .
.
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 记
记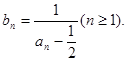
 的通项公式及数列
的通项公式及数列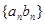 的前n项和
的前n项和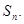
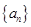 的前n项和记为
的前n项和记为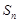 ,
,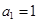 ,点
,点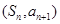 在直线
在直线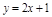 上,n∈N*.
上,n∈N*.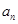 ;
;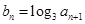 ,
,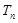 是数列
是数列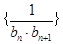 的前n项和,求
的前n项和,求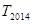 的值.
的值.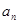 }的前n项和为
}的前n项和为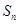 ,
,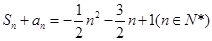 .
.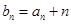 ,证明:数列
,证明:数列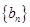 是等比数列;
是等比数列;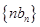 的前
的前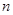 项和
项和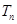 ;
;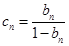 ,数列
,数列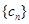 的前
的前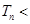
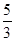 .
.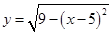 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该数列的公比的数是( )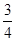
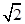
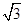
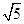
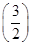 n-1
n-1