题目内容
数列{an}中,a1=3,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列.
(1)求c的值;
(2)求数列{an}的通项公式.
(1)求c的值;
(2)求数列{an}的通项公式.
(1)c=0或c=3(2)an=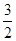 (n2-n+2)
(n2-n+2)
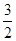 (n2-n+2)
(n2-n+2)(1)a1=3,a2=3+c,a3=3+3c,
∵a1,a2,a3成等比数列,∴(3+c)2=3(3+3c),
解得c=0或c=3.
当c=0时,a1=a2=a3,不符合题意,舍去,故c=3.
(2)当n≥2时,由a2-a1=c,a3-a2=2c,…,an-an-1=(n-1)c,
则an-a1=[1+2+…+(n-1)]c=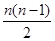 c.
c.
又∵a1=3,c=3,∴an=3+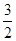 n(n-1)=
n(n-1)=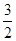 (n2-n+2)(n=2,3,…).
(n2-n+2)(n=2,3,…).
当n=1时,上式也成立,∴an=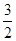 (n2-n+2).
(n2-n+2).
∵a1,a2,a3成等比数列,∴(3+c)2=3(3+3c),
解得c=0或c=3.
当c=0时,a1=a2=a3,不符合题意,舍去,故c=3.
(2)当n≥2时,由a2-a1=c,a3-a2=2c,…,an-an-1=(n-1)c,
则an-a1=[1+2+…+(n-1)]c=
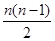 c.
c.又∵a1=3,c=3,∴an=3+
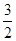 n(n-1)=
n(n-1)=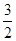 (n2-n+2)(n=2,3,…).
(n2-n+2)(n=2,3,…).当n=1时,上式也成立,∴an=
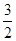 (n2-n+2).
(n2-n+2).
练习册系列答案
相关题目
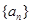 满足
满足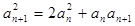 , 且
, 且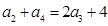 ,其中
,其中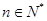 .
.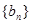 满足
满足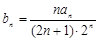 ,是否存在正整数
,是否存在正整数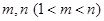 ,使得
,使得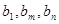 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的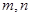 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。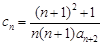 ,记数列
,记数列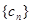 的前
的前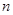 项和为
项和为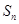 ,其中
,其中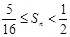 。
。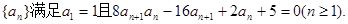 记
记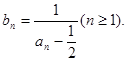
 的通项公式及数列
的通项公式及数列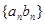 的前n项和
的前n项和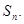
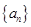 的前n项和记为
的前n项和记为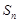 ,
,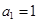 ,点
,点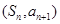 在直线
在直线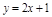 上,n∈N*.
上,n∈N*.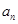 ;
;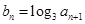 ,
,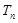 是数列
是数列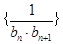 的前n项和,求
的前n项和,求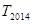 的值.
的值.