题目内容
【题目】已知函数f(x)= ![]() +
+ ![]() ,则下列命题中正确命题的序号是 .
,则下列命题中正确命题的序号是 .
①f(x)是偶函数;
②f(x)的值域是[ ![]() ,2];
,2];
③当x∈[0, ![]() ]时,f(x)单调递增;
]时,f(x)单调递增;
④当且仅当x=2kπ± ![]() (k∈Z)时,f(x)=
(k∈Z)时,f(x)= ![]() .
.
【答案】①②④
【解析】解:对于①,由于f(﹣x)= ![]() +
+ ![]() =f(x),故正确;
=f(x),故正确;
对于②,由题意函数f(x)= ![]() +
+ ![]() =|sin
=|sin ![]() +cos
+cos ![]() |+|sin
|+|sin ![]() ﹣cos
﹣cos ![]() |=
|= 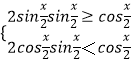 ,
,
所以:在x= ![]() +kπ(k∈Z)时,函数图象位于最低点,
+kπ(k∈Z)时,函数图象位于最低点,
该函数取得最小值 ![]() ,当且仅当x=kπ(k∈Z)时,函数图象位于最高点为2,故正确;
,当且仅当x=kπ(k∈Z)时,函数图象位于最高点为2,故正确;
对于③,当x∈[0, ![]() ]时,
]时, ![]() ∈[0,
∈[0, ![]() ],可得cos
],可得cos ![]() ≥sin
≥sin ![]() ,
,
由题意函数f(x)= ![]() +
+ ![]() =|sin
=|sin ![]() +cos
+cos ![]() |+|sin
|+|sin ![]() ﹣cos
﹣cos ![]() |=2cos
|=2cos ![]() ,
,
由余弦函数的性质可得:f(x)=2cos ![]() ,当x∈[0,
,当x∈[0, ![]() ]时,f(x)单调递减,故错误;
]时,f(x)单调递减,故错误;
对于④,当x=2kπ± ![]() (k∈Z)时,可得sinx=±1,可得:f(x)=
(k∈Z)时,可得sinx=±1,可得:f(x)= ![]() .
.
反之,当f(x)= ![]() 时,函数图象位于最低点,x=
时,函数图象位于最低点,x= ![]() +2kπ(k∈Z),故正确;
+2kπ(k∈Z),故正确;
所以答案是:①②④.

【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.