题目内容
【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
【答案】
(1)解:当x∈[0,3]时,由于f(x)=2x2﹣3x+1图象的对称轴为 ![]() ,且开口向上,
,且开口向上,
可知 ![]() ,f(x)max=f(3)=10,
,f(x)max=f(3)=10,
所以f(x)的值域 ![]() ;
;
当x∈[0,3]时, ![]() ,
, ![]() ;所以当k>0时,g(x)的值域
;所以当k>0时,g(x)的值域 ![]() ;
;
所以当k<0时,g(x)的值域 ![]() ;
;
又∵AB,所以 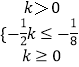 或
或 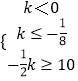 ;
;
即 k≥10或k≤﹣20;
(2)解:∵f(sinx)+sinx﹣a=0,所以2sin2x﹣2sinx+1﹣a=0在x∈[0,2π)上恰有两个解,
设t=sinx,则t∈[﹣1,1],令h(t)=2t2﹣2t+1﹣a,
①当t∈(﹣1,1)时,由题意h(t)=0恰有一个解或者有两个相等的解,
即h(﹣1)h(﹣1)<0或△=4﹣8(1﹣a)=0,即1<a<5或 ![]() ;
;
②若t=﹣1是方程2t2﹣2t+1﹣a=0的一个根,此时a=5,且方程的另一个根为t=2,于是sinx=﹣1或sinx=2,
因此 ![]() ,不符合题意,故a=5(舍);
,不符合题意,故a=5(舍);
③若t=1是方程2t2﹣2t+1﹣a=0的一个根,此时a=1,且方程的另一个根为t=0,于是sinx=1或sinx=0,
因此x=0或 ![]() 或π,不符合题意,故a=1(舍);
或π,不符合题意,故a=1(舍);
综上,a的取值范围是1<a<5或 ![]()
【解析】(1)根据二次函数和正弦函数的图象与性质,分别求出f(x)、g(x)在区间[0,3]上的最值即得值域A、B;再根据AB求出k的取值范围;(2)根据f(sinx)+sinx﹣a=0在x∈[0,2π)上恰有两个解,利用换元法设t=sinx,t∈[﹣1,1],构造函数h(t)=2t2﹣2t+1﹣a,讨论t的取值范围,从而求出实数a的取值范围.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案