题目内容
已知函数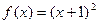
(1)当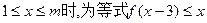 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(2)在曲线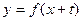 上存在两点关于直线
上存在两点关于直线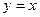 对称,求t的取值范围;
对称,求t的取值范围;
(3)在直线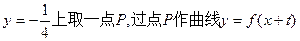 的两条切线l1、l2,
的两条切线l1、l2,
求证:l1⊥l2
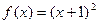
(1)当
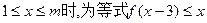 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;(2)在曲线
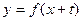 上存在两点关于直线
上存在两点关于直线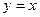 对称,求t的取值范围;
对称,求t的取值范围;(3)在直线
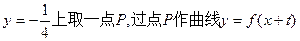 的两条切线l1、l2,
的两条切线l1、l2,求证:l1⊥l2
(Ⅰ)m的最大值为4 (Ⅱ)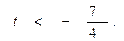
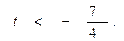
(1)直线y=x与曲线
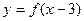 的交点可由
的交点可由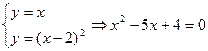
求得交点为(1,1)和(4,4),此时
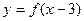 在区间[1,4]上图象在直线y=x的下面,即
在区间[1,4]上图象在直线y=x的下面,即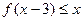 恒成立,所以m的最大值为4。
恒成立,所以m的最大值为4。(2)设曲线上关于直线y=x的对称点为A(
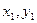 )和B(
)和B(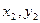 ),线段AB的中点M(
),线段AB的中点M(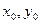 ),直线AB的方程为:
),直线AB的方程为: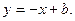
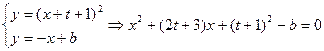
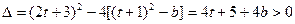 (1分)
(1分)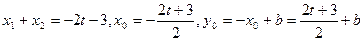
又因为AB中点在直线y=x上,所以
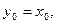
得
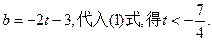 9分
9分(3)设P的坐标为
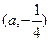 ,过P的切线方程为:
,过P的切线方程为: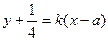 ,则有
,则有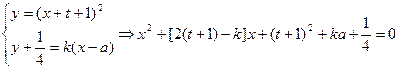
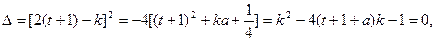
直线
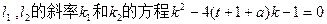 的两根,
的两根,则
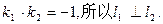 14分
14分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 为原点的直角坐标系中,点
为原点的直角坐标系中,点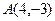 为
为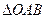 的直角顶点,若
的直角顶点,若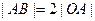 ,且点
,且点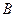 的纵坐标大于0
的纵坐标大于0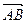 的坐标;
的坐标;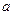 ,使得抛物线
,使得抛物线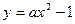 上总有关于直线
上总有关于直线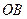 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数 上有一点
上有一点 ,它到焦点的距离等于
,它到焦点的距离等于 ,求实数
,求实数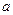 与
与 的值.
的值.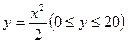 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.