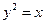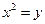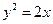题目内容
正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个正三角形的边长.
|AB|=2y1=4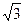 p.
p.
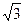 p.
p.如图,设正△OAB的顶点A、B在抛物线上,且它们的坐标分别为(x1,y1)和(x2,y2),则y12=2px1,y22=2px2,又|OA|=|OB|,

∴x12+y12=x22+y22,即x12-x22+2px1-2px2=0.
∴(x1-x2)(x1+x2+2p)=0.∵x1>1,x2>0,2p>0,∴x1=x2.由此可得|y1|=|y2|,即线段AB关于x轴对称.
由于AB垂直于x轴,且∠AOx=30°,∴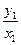 =tan30°=
=tan30°=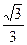 .
.
而y12=2px1,∴y1=2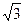 p.于是|AB|=2y1=4
p.于是|AB|=2y1=4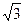 p.
p.

∴x12+y12=x22+y22,即x12-x22+2px1-2px2=0.
∴(x1-x2)(x1+x2+2p)=0.∵x1>1,x2>0,2p>0,∴x1=x2.由此可得|y1|=|y2|,即线段AB关于x轴对称.
由于AB垂直于x轴,且∠AOx=30°,∴
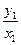 =tan30°=
=tan30°=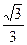 .
.而y12=2px1,∴y1=2
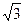 p.于是|AB|=2y1=4
p.于是|AB|=2y1=4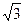 p.
p.
练习册系列答案
相关题目
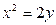 上距
上距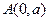 (
(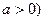 最近的点恰好是顶点的充要条件是什么
最近的点恰好是顶点的充要条件是什么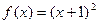
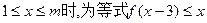 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;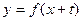 上存在两点关于直线
上存在两点关于直线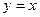 对称,求t的取值范围;
对称,求t的取值范围;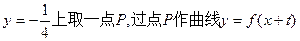 的两条切线l1、l2,
的两条切线l1、l2,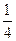 x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.
x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.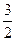 p D.x=
p D.x=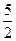 p
p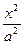 -y2=1(a>0)的一条准线与抛物线y2=-6x的准线重合,则该双曲线的离心率为( )
-y2=1(a>0)的一条准线与抛物线y2=-6x的准线重合,则该双曲线的离心率为( )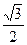
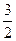
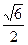
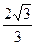
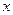 轴上,且经过点
轴上,且经过点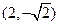 的抛物线的方程为( )
的抛物线的方程为( )