题目内容
在以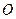 为原点的直角坐标系中,点
为原点的直角坐标系中,点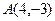 为
为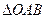 的直角顶点,若
的直角顶点,若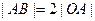 ,且点
,且点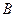 的纵坐标大于0
的纵坐标大于0
(1)求向量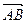 的坐标;
的坐标;
(2)是否存在实数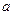 ,使得抛物线
,使得抛物线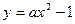 上总有关于直线
上总有关于直线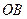 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数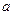 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
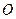 为原点的直角坐标系中,点
为原点的直角坐标系中,点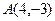 为
为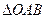 的直角顶点,若
的直角顶点,若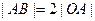 ,且点
,且点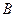 的纵坐标大于0
的纵坐标大于0(1)求向量
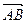 的坐标;
的坐标;(2)是否存在实数
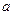 ,使得抛物线
,使得抛物线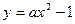 上总有关于直线
上总有关于直线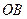 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数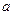 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.(1) (2)当
(2)当 时,抛物线
时,抛物线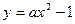 上总有关于直线
上总有关于直线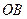 对称的两个点
对称的两个点
 (2)当
(2)当 时,抛物线
时,抛物线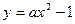 上总有关于直线
上总有关于直线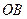 对称的两个点
对称的两个点 (1)设
则由 ,得
,得 ……(4分)
……(4分)
解得 或
或 ……(5分)
……(5分)
因为
所以 ,
,
故 ……(7分)
……(7分)
(2) 设 为抛物线上关于直线
为抛物线上关于直线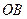 对称的两点,
对称的两点,
则 , 又因为
, 又因为
可得 …………(10分)
…………(10分)
即 为方程
为方程 的两个相异实根
的两个相异实根
于是,由 ,可得
,可得
故当 时,抛物线
时,抛物线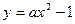 上总有关于直线
上总有关于直线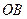 对称的两个点…(13分)
对称的两个点…(13分)

则由
 ,得
,得 ……(4分)
……(4分)解得
 或
或 ……(5分)
……(5分)因为

所以
 ,
,
故
 ……(7分)
……(7分)(2) 设
 为抛物线上关于直线
为抛物线上关于直线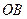 对称的两点,
对称的两点,则
 , 又因为
, 又因为
可得
 …………(10分)
…………(10分)即
 为方程
为方程 的两个相异实根
的两个相异实根于是,由
 ,可得
,可得
故当
 时,抛物线
时,抛物线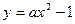 上总有关于直线
上总有关于直线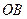 对称的两个点…(13分)
对称的两个点…(13分)
练习册系列答案
相关题目
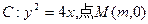 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线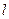 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。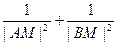 恒为定值。
恒为定值。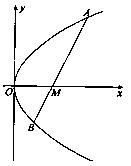
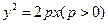 的焦点与椭圆
的焦点与椭圆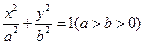 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为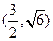 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点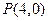 的直线与抛物线交于点
的直线与抛物线交于点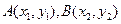 ,求
,求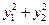 的最小值
的最小值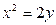 上距
上距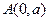 (
(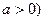 最近的点恰好是顶点的充要条件是什么
最近的点恰好是顶点的充要条件是什么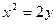
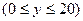 ,在杯中放入一个球,要使球触及酒杯的底部,则球的半径
,在杯中放入一个球,要使球触及酒杯的底部,则球的半径 的取值范围是 。
的取值范围是 。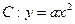 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.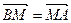 ,求点M的轨迹方程.
,求点M的轨迹方程.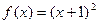
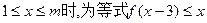 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;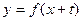 上存在两点关于直线
上存在两点关于直线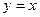 对称,求t的取值范围;
对称,求t的取值范围;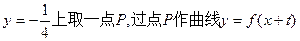 的两条切线l1、l2,
的两条切线l1、l2,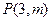 在以点
在以点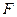 为焦点的抛物线
为焦点的抛物线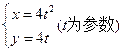 上,则
上,则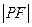 等于 .
等于 .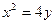 的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且 。
。