题目内容
设A(x1,y1)、B(x2,y2)两点在抛物线y=2x2上,l是AB的垂直平分线.
(1)当且仅当x1+x2取何值时,直线l经过抛物线的焦点F?证明你的结论.
(2)当直线l的斜率为2时,求l在y轴上的截距的取值范围.
(1)当且仅当x1+x2取何值时,直线l经过抛物线的焦点F?证明你的结论.
(2)当直线l的斜率为2时,求l在y轴上的截距的取值范围.
l在y轴上截距的取值范围是(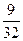 ,+∞).
,+∞).
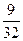 ,+∞).
,+∞).(1)F∈l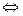 |FA|=|FB|
|FA|=|FB|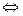 A、B两点到抛物线准线的距离相等
A、B两点到抛物线准线的距离相等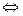 y1=y2
y1=y2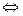 x12=x22
x12=x22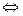 (x1+x2)
(x1+x2)
(x1-x2)=0,由A、B为两点,∴x1≠x2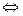 x1+x2=0.
x1+x2=0.
故x1+x2=0时,直线l经过焦点F.
(2)设l:y=2x+b,
∵l⊥AB,
设AB:y=-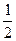 x+m,联立y=2x2,
x+m,联立y=2x2,
∴2x2+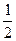 x-m=0,
x-m=0,
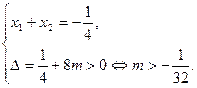
设AB中点N(x0,y0),
则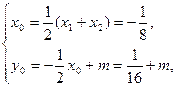
由点N∈l,∴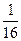 +m=-
+m=-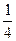 +b,
+b,
b= +m>
+m> -
- =
=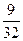 .
.
∴l在y轴上截距的取值范围是(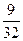 ,+∞).
,+∞).
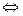 |FA|=|FB|
|FA|=|FB|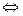 A、B两点到抛物线准线的距离相等
A、B两点到抛物线准线的距离相等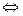 y1=y2
y1=y2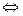 x12=x22
x12=x22 (x1+x2)
(x1+x2)(x1-x2)=0,由A、B为两点,∴x1≠x2
 x1+x2=0.
x1+x2=0.故x1+x2=0时,直线l经过焦点F.
(2)设l:y=2x+b,
∵l⊥AB,
设AB:y=-
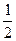 x+m,联立y=2x2,
x+m,联立y=2x2,∴2x2+
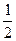 x-m=0,
x-m=0,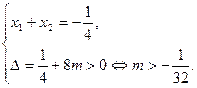
设AB中点N(x0,y0),
则
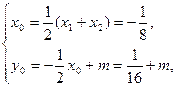
由点N∈l,∴
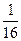 +m=-
+m=-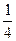 +b,
+b,b=
 +m>
+m> -
- =
=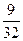 .
.∴l在y轴上截距的取值范围是(
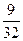 ,+∞).
,+∞).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
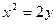
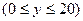 ,在杯中放入一个球,要使球触及酒杯的底部,则球的半径
,在杯中放入一个球,要使球触及酒杯的底部,则球的半径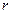 的取值范围是 。
的取值范围是 。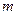 ),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3
),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3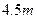 ,此车是否能通过隧道?并说明理由.
,此车是否能通过隧道?并说明理由.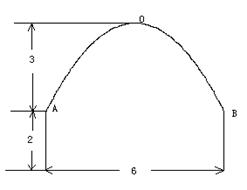
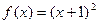
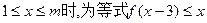 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;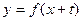 上存在两点关于直线
上存在两点关于直线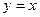 对称,求t的取值范围;
对称,求t的取值范围;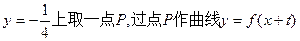 的两条切线l1、l2,
的两条切线l1、l2,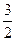 p D.x=
p D.x=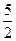 p
p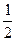 =0的距离为________________.
=0的距离为________________.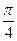 的直线与抛物线y2=2px,x2=2py(p>0)都相交于两点,那么a的取值范围是( )
的直线与抛物线y2=2px,x2=2py(p>0)都相交于两点,那么a的取值范围是( )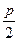
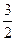 ,±
,±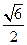 )
)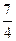 ,±
,±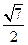 )
)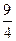 ,±
,±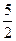 ,±
,± )
)