题目内容
已知f(x)=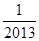 +log2
+log2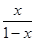 ,则f
,则f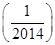 +f
+f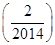 +…+f
+…+f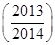 的值为( )
的值为( )
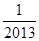 +log2
+log2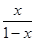 ,则f
,则f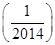 +f
+f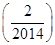 +…+f
+…+f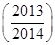 的值为( )
的值为( )| A.1 | B.2 | C.2 013 | D.2 014 |
A
对任意0<x<1,可得f(x)+f(1-x)=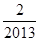 .
.
设S=f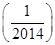 +f
+f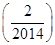 +…+f
+…+f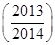
则S=f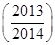 +f
+f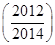 +…+f
+…+f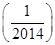
于是2S=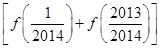 +
+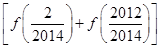 +…+
+…+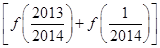 =
=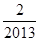 ×2 013=2,所以S=1.
×2 013=2,所以S=1.
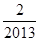 .
.设S=f
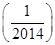 +f
+f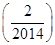 +…+f
+…+f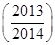
则S=f
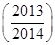 +f
+f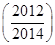 +…+f
+…+f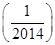
于是2S=
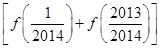 +
+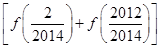 +…+
+…+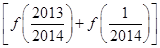 =
=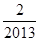 ×2 013=2,所以S=1.
×2 013=2,所以S=1.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的取值范围;
的取值范围; n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列. (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
. (
( )是常数数列;
)是常数数列; 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 (
(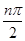 -bn·cos2
-bn·cos2 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增. 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;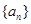 中,
中,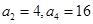 .
.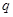 ;
;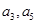 分别为等差数列
分别为等差数列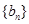 的第3项和第5项,求数列
的第3项和第5项,求数列 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 =
=

