题目内容
已知 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
.
(1)证明:数列 (
( )是常数数列;
)是常数数列;
(2)确定 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 是单调递增数列;
是单调递增数列;
(3)证明:当 时,弦
时,弦 (
( )的斜率随
)的斜率随 单调递增
单调递增
 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
.(1)证明:数列
 (
( )是常数数列;
)是常数数列;(2)确定
 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 是单调递增数列;
是单调递增数列;(3)证明:当
 时,弦
时,弦 (
( )的斜率随
)的斜率随 单调递增
单调递增(1)证明见解析;(2)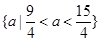 ;(3)证明见解析.
;(3)证明见解析.
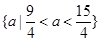 ;(3)证明见解析.
;(3)证明见解析.试题分析:(1)由已知有
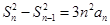 ,即
,即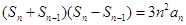 ,而数列中
,而数列中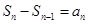 ,因此已知式变为
,因此已知式变为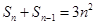 ,这是
,这是 的递推式,我们可以用
的递推式,我们可以用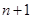 代换其中的
代换其中的 得
得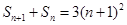 ,两式相减,可把
,两式相减,可把 转化为
转化为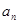 的递推式
的递推式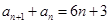 ,出现了数列相邻项的和时,同样再把这个式子中的
,出现了数列相邻项的和时,同样再把这个式子中的 用
用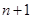 代换,得
代换,得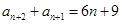 ,两式相减,得
,两式相减,得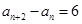 ,代入可证得
,代入可证得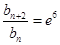 为常数;(2)由(1)说明数列
为常数;(2)由(1)说明数列 的奇数项,偶数项分别成等差数列且公差为6,因此要使数列
的奇数项,偶数项分别成等差数列且公差为6,因此要使数列 为递增数列,只要有
为递增数列,只要有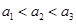 即可,解这个不等式可得
即可,解这个不等式可得 的范围;(3)
的范围;(3)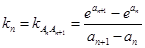 ,本题就是要证明
,本题就是要证明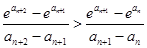 ,考虑到数列
,考虑到数列 是递增数列,函数
是递增数列,函数 是增函数,因此只要证
是增函数,因此只要证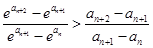 ,即证
,即证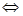
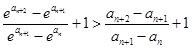
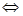
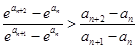
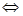
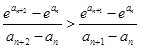 ,这就是
,这就是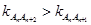 ,从
,从 的图象上可算出这个结论是正确的,从数上看,取
的图象上可算出这个结论是正确的,从数上看,取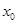 为常数,
为常数,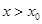 ,我们要证明函数
,我们要证明函数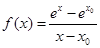 为增函数,这用导数的知识可证.
为增函数,这用导数的知识可证.(1)当
 时,由已知得
时,由已知得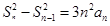 ,
,因为
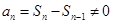 ,所以
,所以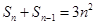 . ①
. ①于是
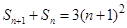 , ②
, ②由②-①得
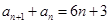 , ③
, ③于是
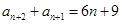 , ④
, ④由④-③得
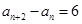 . ⑤
. ⑤所以
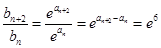 ,即数列
,即数列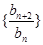
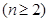 是常数数列.
是常数数列.(2)由①有
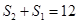 ,所以
,所以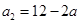 .由③有
.由③有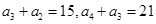 ,所以
,所以 .而⑤表明数列
.而⑤表明数列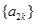 和
和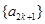 分别是以
分别是以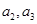 为首项,6为公差的等差数列,
为首项,6为公差的等差数列,所以
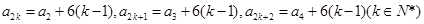 ,
,数列
 是单调递增数列
是单调递增数列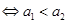 ,且
,且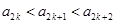 对任意的
对任意的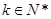 成立,
成立,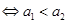 且
且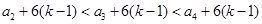
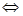
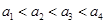
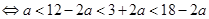
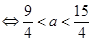 .
.即所求
 取值集合为
取值集合为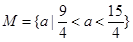 .
.(3)解法一:弦
 的斜率为
的斜率为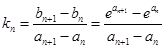 ,
,任取
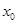 ,设函数
,设函数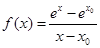 ,则
,则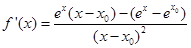 ,
,记
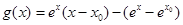 ,则
,则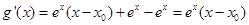 ,
,当
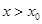 时,
时,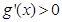 ,
,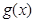 在
在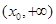 上为增函数,
上为增函数,当
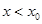 时,
时,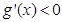 ,
,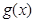 在
在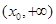 上为减函数,
上为减函数,所以
 时,
时,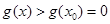 ,从而
,从而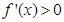 ,所以
,所以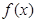 在
在 和
和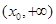 上都是增函数.
上都是增函数.由(2)知
 时,数列
时,数列 单调递增,
单调递增,取
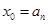 ,因为
,因为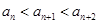 ,所以
,所以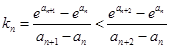 ,
,取
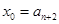 ,因为
,因为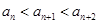 ,所以
,所以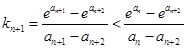 ,
,所以
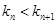 ,即弦
,即弦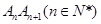 的斜率随
的斜率随 单调递增.
单调递增.解法二:设函数
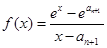 ,同解法一得,
,同解法一得,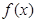 在
在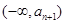 和
和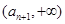 上都是增函数,
上都是增函数,所以
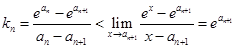 ,
,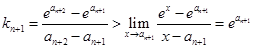 ,
,故
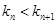 ,即弦
,即弦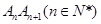 的斜率随
的斜率随 单调递增.
单调递增.
练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
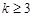 ,若项数为
,若项数为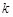 的数列
的数列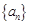 满足:对任意的
满足:对任意的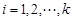 ,均有
,均有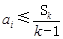 (其中
(其中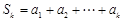 ),则称数列
),则称数列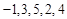 和
和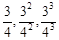 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;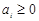 对
对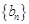 是公差为
是公差为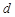 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数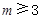 ,
,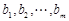
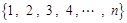
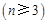 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为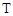 子集,记
子集,记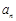 .
.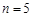 时,写出所有
时,写出所有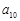 ;
;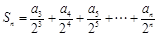 ,求证:
,求证: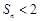




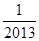 +log2
+log2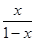 ,则f
,则f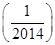 +f
+f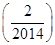 +…+f
+…+f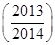 的值为( )
的值为( )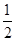 ,
,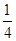 ,…,
,…,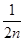 ,….是( )
,….是( )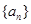 中,
中,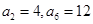 ,则
,则



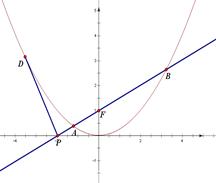
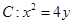 ,直线
,直线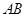 过抛物线
过抛物线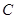 的焦点
的焦点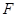 ,交
,交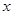 轴于点
轴于点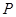 .
.
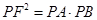 ;
;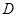 (异于原点),
(异于原点),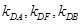 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;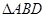 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.