题目内容
设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(1) 若当n=10时,Sn取到最小值,求 的取值范围;
的取值范围;
(2) 证明: n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(1) 若当n=10时,Sn取到最小值,求
 的取值范围;
的取值范围;(2) 证明:
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.见解析
(1)解:由题意可知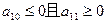 ,所以
,所以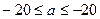 (2)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即
(2)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即 .因此
.因此
a2+2ma+2m(m+1)=0, 要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列.
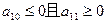 ,所以
,所以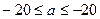 (2)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即
(2)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即 .因此
.因此a2+2ma+2m(m+1)=0, 要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
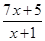 ,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).
,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).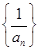 是等差数列;
是等差数列;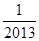 +log2
+log2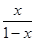 ,则f
,则f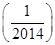 +f
+f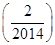 +…+f
+…+f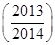 的值为( )
的值为( )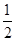 ,
,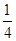 ,…,
,…,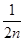 ,….是( )
,….是( )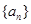 中,
中,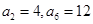 ,则
,则



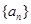 中,
中,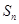 是它的前n项之和,且
是它的前n项之和,且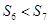 ,
,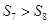 ,则:
,则: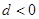 ; ②
; ②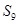 一定小于
一定小于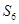 ;
;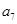 是各项中最大的一项; ④
是各项中最大的一项; ④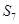 一定是
一定是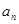 }的前
}的前 项和
项和 ,则
,则 的值为 ( )
的值为 ( ) 



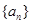 中,若
中,若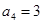 ,则
,则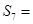 .
.