题目内容
16.已知定义域为R的函数f(x)满足:(1)当x∈(0,1]时,f(x)=x2;(2)f(x+1)=2f(x),则$\frac{f(x)}{{2}^{x}}$的最大值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
分析 由题意,(1)当x∈(0,1]时,f(x)=x2,$\frac{f(x)}{{2}^{x}}$=$\frac{{x}^{2}}{{2}^{x}}$;(2)当x∈(n,n+1],(n∈N*)时,$\frac{f(x)}{{2}^{x}}$=$\frac{(x-n)^{2}}{{2}^{x-n}}$;从而可判断$\frac{f(x)}{{2}^{x}}$是周期为1的函数,再利用导数求最值即可.
解答 解:(1)当x∈(0,1]时,f(x)=x2,$\frac{f(x)}{{2}^{x}}$=$\frac{{x}^{2}}{{2}^{x}}$;
(2)当x∈(n,n+1],(n∈N*)时,
f(x)=2f(x-1)=22f(x-2)
=2nf(x-n)=2n•(x-n)2;
故$\frac{f(x)}{{2}^{x}}$=$\frac{{2}^{n}(x-n)^{2}}{{2}^{x}}$=$\frac{(x-n)^{2}}{{2}^{x-n}}$;
故$\frac{f(x)}{{2}^{x}}$是周期为1的函数,
故只需讨论x∈(0,1]时的最大值即可;
当x∈(0,1]时,令g(x)=$\frac{{x}^{2}}{{2}^{x}}$,
则g′(x)=$\frac{2x•{2}^{x}-ln2•{2}^{x}•{x}^{2}}{{(2}^{x})^{2}}$=x•$\frac{2-xln2}{{2}^{x}}$>0;
故g(x)=$\frac{{x}^{2}}{{2}^{x}}$在(0,1]上是增函数;
故gmax(x)=g(1)=$\frac{1}{2}$;
故选A.
点评 本题考查了函数的性质的判断与应用,同时考查了导数的综合应用,属于中档题.

练习册系列答案
相关题目
13.已知f(x+1)是周期为2的奇函数,当-1≤x≤0时,f(x)=-2x(x+1),则f(-$\frac{3}{2}$)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
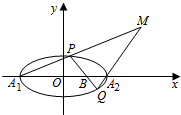 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.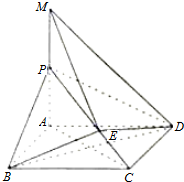
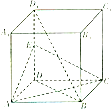 如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点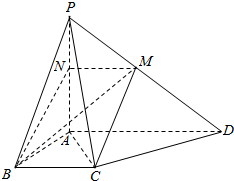 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).