题目内容
8.已知函数f(x)=lnx,g(x)=ax2-x(a≥0)(1)a=0时,令h(x)=f(x)g(x),求h(x)的极值.
(2)当a=1时,求证:f(x)≤g(x)
(3)若y=f(x)与y=g(x)的图象交于点M,N两点,过线段MN的中点作x轴的垂线分别与f(x)的图象和g(x)的图象交于S,T点,以S为切点作f(x)的切线l1,以t为切点作g(x)的切线l2.是否存在实数a使得l1∥l2,如果存在,求出a的值;如果不存在,请说明理由.
分析 (1)利用导数和函数的极值的关系即可求出;
(2)构造函数,h(x)=g(x)-f(x),利用导数求出函数的最小值即可;
(3)不妨设M(x1,y1),N(x2,y2),且x1>x2,求出MN中点的坐标,分别求出以S、T为切点的切线l1,l2的斜率,假设kS=kT,则a(x1+x2)-1=$\frac{2}{{x}_{1}+{x}_{2}}$,
化为$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$=ln$\frac{{x}_{1}}{{x}_{2}}$.令$\frac{{x}_{1}}{{x}_{2}}$=t>1,可得lnt=$\frac{2(t-1)}{t+1}$=2-$\frac{4}{t+1}$,令u(t)=lnt+$\frac{4}{t+1}$-2,利用导数研究其单调性即可判断出.
解答 解:(1)a=0时,h(x)=f(x)g(x)=-xlnx,其定义域为(0,+∞),
∴h′(x)=-lnx-1,
令h′(x)=0,解得a=$\frac{1}{e}$,
当h′(x)>0时,即0<x<$\frac{1}{e}$,函数h(x)单调递增,
当h′(x)<0时,即x>$\frac{1}{e}$,函数h(x)单调递减,
∴当x=$\frac{1}{e}$,h(x)取得极大值$\frac{1}{e}$,无极小值;
(Ⅱ)当a=1时,h(x)=g(x)-f(x)=x2-x-lnx,
∴h′(x)=2x-1-$\frac{1}{x}$=$\frac{2{x}^{2}-x-1}{x}$=$\frac{(2x+1)(x-1)}{x}$,
令h′(x)=0,解得x=1,
当x>1,h′(x)>0,h(x)递增;
当0<x<1时,h′(x)<0,h(x)递减.
∴h(x)min=h(1)=0,
即x>0时,h(x)≥0恒成立,
∴当a=1时,f(x)≤g(x);
不妨设M(x1,y1),N(x2,y2),且x1>x2,则MN中点的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
以S、T为切点的切线l1,l2的斜率分别为kS=f′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{2}{{x}_{1}+{x}_{2}}$,
kT=g′($\frac{{x}_{1}+{x}_{2}}{2}$)=a(x1+x2)-1,
假设kS=kT,则a(x1+x2)-1=$\frac{2}{{x}_{1}+{x}_{2}}$,
∴a(x12-x22)-(x1-x2)=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$,
∴$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$=y1-y2=lnx1-lnx2,化为$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$=ln$\frac{{x}_{1}}{{x}_{2}}$.
令$\frac{{x}_{1}}{{x}_{2}}$=t>1,可得lnt=$\frac{2(t-1)}{t+1}$=2-$\frac{4}{t+1}$,
令u(t)=lnt+$\frac{4}{t+1}$-2,
∴u′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴u(t)在(1,+∞)上单调递增,
∴u(t)>u(1)=0,
∴lnt=$\frac{2(t-1)}{t+1}$不成立,
因此不存在a使得l1∥l2.
点评 本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义、中点坐标公式、平行线与斜率的关系等基础知识与基本技能方法,考查了等价转化方法、换元法,考查了推理能力与计算能力,属于难题

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )| A. | f(-1) | B. | f(-2) | C. | f(1) | D. | f(2) |
| A. | 3$\root{3}{9}$ | B. | 1+2$\sqrt{2}$ | C. | 7 | D. | 6 |
| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
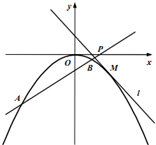 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.