题目内容
1.如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.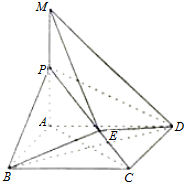
(1)证明:BD⊥平面PAC;
(2)若点M在线段AP的延长线上且P为MA的中点,PA=1,AD=2,求二面角
B-ED-M的余弦值.
分析 (1)由题设条件及图知,可先由线面垂直的性质证出PA⊥BD与PC⊥BD,再由线面垂直的判定定理证明线面垂直即可;
(2)先找出ABCD为正方形,得到AB=AD=2,以A点为原点,AB、AD、AP为x、y、z轴,建立空间直角坐标系,求出平面BED、平面MDE的法向量,从而求出二面角的余弦值.
解答 (1)证明:∵PA⊥平面ABCD,
∴PA⊥BD,
∵PC⊥平面BDE,
∴PC⊥BD,又PA∩PC=P,
∴BD⊥平面PAC,
(2)解:由(1)可知BD⊥平面PAC,而AC?平面PAC,
∴BD⊥AC,而ABCD为矩形,
∴ABCD为正方形,∴AB=AD=2,
以A点为原点,AB、AD、AP为x、y、z轴,建立空间直角坐标系A-BDP,
如图示:
则M(0,0,2)、D(0,2,0)、C(2,2,0),
平面BED的一个法向量为${\overrightarrow{n}}_{2}$=$\overrightarrow{PC}$=(2,2,-1),$\overrightarrow{MD}$=(0,2,-2),
设$\overrightarrow{CE}$=λ$\overrightarrow{CP}$,$\overrightarrow{DE}$=$\overrightarrow{DC}$+λ$\overrightarrow{CP}$=(2-2λ,-2λ,λ),$\overrightarrow{DE}$•$\overrightarrow{PC}$=0,
λ=$\frac{4}{9}$,$\overrightarrow{DE}$=($\frac{10}{9}$,-$\frac{8}{9}$,$\frac{4}{9}$),
设平面MDE的一个法向量为$\overrightarrow{{n}_{1}}$={x,y,z},
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{DE}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{MD}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{\frac{10}{9}x-\frac{8}{9}y+\frac{4}{9}z=0}\\{2y-2z=0}\end{array}\right.$,
令z=5,∴$\overrightarrow{{n}_{1}}$=(2,5,5),
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{|\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}|}{|\overrightarrow{{n}_{1}}|•|\overrightarrow{{n}_{2}}|}$=$\frac{9}{3×3\sqrt{6}}$=$\frac{\sqrt{6}}{6}$,
∴二面角 B-ED-M的余弦值为:-$\frac{\sqrt{6}}{6}$.
点评 本题考查二面角的平面角的求法及线面垂直的判定定理与性质定理,属于立体几何中的基本题型,作出坐标系通过法向量求二面角的平面角是常用的方法.

| A. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{3}$] | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{3}}{3}$] |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
(Ⅰ)当a=1时,求f(x)的最大值;
(Ⅱ)当x∈(-∞,0)∪(0,+∞)时,$\frac{f(x)}{x}$<1恒成立,证明:a=1.
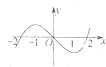 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )| A. | f(-1) | B. | f(-2) | C. | f(1) | D. | f(2) |
 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.