题目内容
12.一个几何体的三视图如图所示(单位:cm),则该几何体的体积等于10cm3.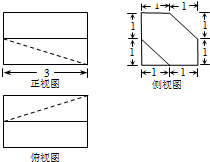
分析 由已知中的三视图,可知该几何体是一个长方体,挖去一个三棱柱和一个三棱锥后所得的组合体,分别求出长方体,三棱柱和三棱锥的体积,相减可得答案.
解答 解:由已知中的三视图,可知该几何体是一个长方体,挖去一个三棱柱和一个三棱锥后所得的组合体,
长方体的体积为:3×2×2=12cm3,
三棱柱的体积为:3×($\frac{1}{2}$×1×1)=$\frac{3}{2}$cm3,
三棱锥的体积为:$\frac{1}{3}$×3×($\frac{1}{2}$×1×1)=$\frac{1}{2}$cm3,
故组合体的体积V=12-$\frac{3}{2}$-$\frac{1}{2}$=10cm3,
故答案为:10.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-3y=0,则它的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
7.在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,离心率为$\sqrt{5}$,则其渐进线方程为( )
| A. | y=$\frac{1}{2}$x | B. | y=±$\frac{1}{2}$x | C. | y=-$\frac{1}{2}$x | D. | y=±2x |
16.已知定义域为R的函数f(x)满足:(1)当x∈(0,1]时,f(x)=x2;(2)f(x+1)=2f(x),则$\frac{f(x)}{{2}^{x}}$的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |