��Ŀ����
11��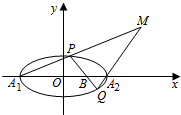 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������l�ķ���Ϊx=$\frac{4\sqrt{3}}{3}$������Ϊ2$\sqrt{3}$��
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������l�ķ���Ϊx=$\frac{4\sqrt{3}}{3}$������Ϊ2$\sqrt{3}$����1������ԲC�ķ��̣�
��2��������B��1��0����ֱ��l����ԲC����P��Q��������ԲC�����Ҷ���A1��A2���㣩����ֱ��PA1��ֱ��QA2�ཻ�ڵ�M��
����M��4��2���������P��Q�����ꣻ
����֤����Mʼ����һ����ֱ���ϣ�
���� ��1������Բ�������ʹ�ʽ��a��b��c�Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2�������ֱ��MA1�ķ��̺���MA2�ķ��̣�������Բ���̣���ý���P��Q�����ꣻ
�����M��x0��y0�������ֱ��MA1�ķ��̺���MA2�ķ��̣�������Բ���̣���ý���P��Q�����꣬���P��Q��B���㹲�ߣ�����kPB=kQB�������������ɵ�x0-4=0��$\frac{{{x}_{0}}^{2}}{4}$+y02=1���ֱ��ǣ����ɵõ���Mʼ����һ����ֱ��x=4�ϣ�
��� �⣺��1����$\left\{\begin{array}{l}{\frac{{a}^{2}}{c}=\frac{4\sqrt{3}}{3}}\\{2c=2\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$����$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=\sqrt{3}}\end{array}\right.$��������ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1��
��2������ΪA1��-2��0����A2��2��0����M��4��2����
����MA1�ķ���Ϊy=$\frac{1}{3}$��x+2��������x2+4y2=4��
x2-4+4[$\frac{1}{3}$��x+2��]2=0������x+2��[��x-2��+$\frac{4}{9}$��x+2��]=0
��ΪA1�ĺ�����Ϊ-2������xP=$\frac{10}{13}$����yP=$\frac{12}{13}$��
���Ե�P������Ϊ��$\frac{10}{13}$��$\frac{12}{13}$����
ͬ���ɵõ�Q������Ϊ��$\frac{6}{5}$��-$\frac{4}{5}$����
��֤�������M��x0��y0����������xM�١�2����ΪA1��-2��0����A2��2��0����
����ֱ��MA1�ķ���Ϊy=$\frac{{y}_{0}}{{x}_{0}+2}$��x+2��������x2+4y2=4��
��x2-4+4[$\frac{{y}_{0}}{{x}_{0}+2}$��x+2��]2=0������x+2��[��x-2��+$\frac{4{{y}_{0}}^{2}}{��{x}_{0}+2��^{2}}$��x+2��]=0
��ΪA1�ĺ�����Ϊ-2��
����xP=$\frac{2-\frac{8{{y}_{0}}^{2}}{��{x}_{0}+2��^{2}}}{1+\frac{4{{y}_{0}}^{2}}{��{x}_{0}+2��^{2}}}$=$\frac{4��{x}_{0}+2��^{2}}{��{x}_{0}+2��^{2}+4{{y}_{0}}^{2}}$-2����yP=$\frac{4��{x}_{0}+2��{y}_{0}}{��{x}_{0}+2��^{2}+4{{y}_{0}}^{2}}$��
�ʵ�P������Ϊ��$\frac{4��{x}_{0}+2��^{2}}{��{x}_{0}+2��^{2}+4{{y}_{0}}^{2}}$-2��$\frac{4��{x}_{0}+2��{y}_{0}}{��{x}_{0}+2��^{2}+4{{y}_{0}}^{2}}$����
ͬ���ɵõ�Q������Ϊ��$\frac{-4��{x}_{0}-2��^{2}}{��{x}_{0}-2��^{2}+4{{y}_{0}}^{2}}$+2��$\frac{-4��{x}_{0}-2��{y}_{0}}{��{x}_{0}-2��^{2}+4{{y}_{0}}^{2}}$��
��ΪP��Q��B���㹲�ߣ�����kPB=kQB��$\frac{{y}_{P}}{{x}_{P}-1}$=$\frac{{y}_{Q}}{{x}_{Q}-1}$��
����$\frac{\frac{4��{x}_{0}+2��{y}_{0}}{��{x}_{0}+2��^{2}+{{y}_{0}}^{2}}}{\frac{4��{x}_{0}+2��^{2}}{��{x}_{0}+2��^{2}+4{{y}_{0}}^{2}}-2-1}$=$\frac{\frac{-4��{x}_{0}-2��{y}_{0}}{��{x}_{0}-2��^{2}+4{{y}_{0}}^{2}}}{\frac{-4��{x}_{0}-2��^{2}}{��{x}_{0}-2��^{2}+4{{y}_{0}}^{2}}+2-1}$����$\frac{��{x}_{0}+2��{y}_{0}}{��{x}_{0}+2��^{2}-12{{y}_{0}}^{2}}$=$\frac{-��{x}_{0}-2��{y}_{0}}{-3��{x}_{0}-2��^{2}+4{{y}_{0}}^{2}}$��
�����⣬y0��0������$\frac{{x}_{0}+2}{��{x}_{0}+2��^{2}-12{{y}_{0}}^{2}}$=$\frac{{x}_{0}-2}{3��{x}_{0}-2��^{2}-4{{y}_{0}}^{2}}$��
��3��x0+2����x0-2��2-4��x0+2��y02=��x0-2����x0+2��2-12��x0-2��y02��
���ԣ�x0-4����$\frac{{{x}_{0}}^{2}}{4}$+y02-1��=0����x0-4=0��$\frac{{{x}_{0}}^{2}}{4}$+y02=1��
��$\frac{{{x}_{0}}^{2}}{4}$+y02=1�����M����Բ�ϣ�P��Q��MΪͬһ�㣬�������⣮
����xM=4������Mʼ���ڶ�ֱ��x=4�ϣ�
���� ���⿼����Բ�ķ��̺����ʣ���Ҫ������Բ�������ʺͷ��̵����ã�����ֱ�߷��̣��ⷽ���㣬ͬʱ�������㹲�ߵ����������黯�����������������������е��⣮

| A�� | y=$\frac{1}{2}$x | B�� | y=��$\frac{1}{2}$x | C�� | y=-$\frac{1}{2}$x | D�� | y=��2x |
| A�� | $\frac{3}{2}$ | B�� | 2 | C�� | 3 | D�� | $\frac{5}{2}$ |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | 1 | D�� | 2 |
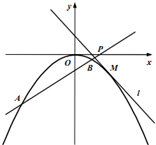 ��֪����C��x2=-2py��p��0������M������C�ϵ�һ�����㣬����M��������C���е�ֱ��l�ķ���Ϊx+y-1=0��
��֪����C��x2=-2py��p��0������M������C�ϵ�һ�����㣬����M��������C���е�ֱ��l�ķ���Ϊx+y-1=0��