题目内容
6.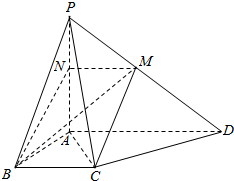 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).(Ⅰ)求证:MN∥BC;
(Ⅱ)求证:CD⊥PC;
(Ⅲ)如果BM⊥AC,求此时$\frac{PM}{PD}$的值.
分析 (Ⅰ)根据线面平行的性质定理即可证明MN∥BC;
(Ⅱ)根据线面垂直的性质定理证明求证:CD⊥PC;
(Ⅲ)根据线面垂直的判定定理证明AC⊥面BEM,即可证明M是PD的中点即可得到结论.
解答 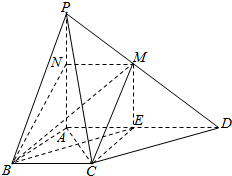 证明:(Ⅰ)∵BC∥AD,BC?平面PAD,AD?平面PAD,
证明:(Ⅰ)∵BC∥AD,BC?平面PAD,AD?平面PAD,
∴BC∥平面PAD,
∵平面PAD∩平面BCMN=MN,
∴BC∥MN,即MN∥BC;
(Ⅱ)取AD中点E,连接CE,BE,
∵AB=BC=$\frac{1}{2}$AD,
∴四边形ABCE为正方形,
∵E是AD的中点,
∴△ACD是等腰直角三角形,
∴AC⊥CD,即CD⊥AC,
∵PA⊥底面ABCD,CD?底面ABCD,
∴PA⊥CD,
∵PA∩AC=A,
∴CD⊥面PAC,
∵PC?面PAC,
∴CD⊥PC.
(Ⅲ)连接BE,则BE∥CD,
∵AC⊥CD,∴AC⊥BE,
若BM⊥AC,
∵BM∩BE=B,
∴AC⊥面BEM,
∵ME?面BEM,
∴AC⊥EM,
∵E是AD的中点,
∴M是PD的中点,
即$\frac{PM}{PD}$=$\frac{1}{2}$.
点评 本题主要考查线面垂直和线面平行的判定和性质,综合考查空间直线和平面的位置关系的判定,要求熟练掌握相应的判定定理和性质定理,考查学生的运算和推理能力.

练习册系列答案
相关题目
16.已知定义域为R的函数f(x)满足:(1)当x∈(0,1]时,f(x)=x2;(2)f(x+1)=2f(x),则$\frac{f(x)}{{2}^{x}}$的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
17.若x,y∈R且满足x+3y=2,则3x+27y+1的最小值是( )
| A. | 3$\root{3}{9}$ | B. | 1+2$\sqrt{2}$ | C. | 7 | D. | 6 |
18.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,设椭圆与双曲线的离心率分别为e1,e2,则e1+e2的取值范围是( )
| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
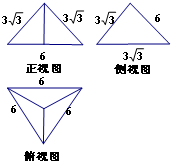 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.