题目内容
5．
如图，正方体ABCD-A1B1C1D1中，E为线段DD1的中点（1）求证：AC⊥平面BDD1
（2）求EA与平面BDD1所成角的正弦值．
分析 （1）由正方体ABCD-A1B1C1D1中，DD1⊥平面ABCD，可证DD1⊥AC，又AC⊥BD，即可证明AC⊥平面BDD1．
（2）设AC∩BD=O，连接EO，由AC⊥平面DD1B，可得∠AEO为EA与平面BDD1所成角．不妨设正方形的边长为2，AO=$\sqrt{2}$，AE=$\sqrt{5}$，即可由sin∠AEO=$\frac{AO}{AE}$求值．
解答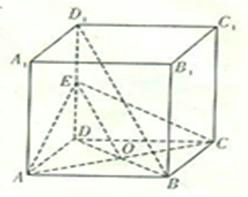 
本题满分为12分
解：（1）证明：∵正方体ABCD-A1B1C1D1中，DD1⊥平面ABCD，
∴DD1⊥AC
又∵在正方向ABCD中，AC⊥BD
∴AC⊥平面BDD1…6分
（2）设AC∩BD=O，连接EO，
∵AC⊥平面DD1B，
∴∠AEO为EA与平面BDD1所成角．
不妨设正方形的边长为2，AO=$\sqrt{2}$，AE=$\sqrt{5}$，
可得：sin∠AEO=$\frac{AO}{AE}$=$\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$…12分．
点评 本题主要考查了直线与平面垂直的判定，直线与平面所成的角，考查了空间想象能力和推论论证能力，属于中档题．
练习册系列答案
相关题目
16．已知定义域为R的函数f（x）满足：（1）当x∈（0，1]时，f（x）=x2；（2）f（x+1）=2f（x），则$\frac{f（x）}{{2}^{x}}$的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 1 | D． | 2 |
13．
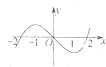设f（x）是一个三次函数，f′（x）为其导函数，如图是函数y=x•f′（x）的图象的一部分，则函数f（x）的极大值是（ ）
设f（x）是一个三次函数，f′（x）为其导函数，如图是函数y=x•f′（x）的图象的一部分，则函数f（x）的极大值是（ ）| A． | f（-1） | B． | f（-2） | C． | f（1） | D． | f（2） |
17．若x，y∈R且满足x+3y=2，则3x+27y+1的最小值是（ ）
| A． | 3$\root{3}{9}$ | B． | 1+2$\sqrt{2}$ | C． | 7 | D． | 6 |