题目内容
【题目】某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.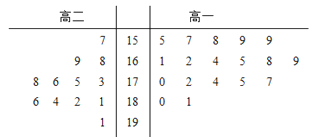
(1)如果从所有运动员中用分层抽样抽取“合格”与“不合格”的人数共10人,问就抽取“合格”人数是多少?
(2)若从所有“合格”运动员中选取2名,用X表示所选运动员来自高一队的人数,试写出X的分布图,并求X的数学期望.
【答案】解:(1)根据茎叶图可得:“合格”的人数有12,“不合格”人数有18,
用分层抽样的方法,每个运动员被抽中的概率是![]() =
=![]() ,
,
所以抽取“合格”人数是12×![]() =4
=4
(2)以题意得:X的值为:0,1,2.
则P(X=0)=![]() =
=![]() =
=![]() ,
,
P(X=1)=![]() =
=![]() =
=![]() ,
,
P(X=2)=![]() =
=![]() =
=![]()
X的分布:
X | 0 | 1 | 2 |
P |
|
|
|
X的数学期望:0×![]() +1x
+1x![]() +2x
+2x![]() =
=![]() =
=![]()
【解析】(1)运用分层抽样求解.
(2)先确定X的值为:0,1,2.再求P(X=0),P(X=1),P(X=2)
列出概率分布,求出数学期望.
【考点精析】根据题目的已知条件,利用茎叶图的相关知识可以得到问题的答案,需要掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
