题目内容
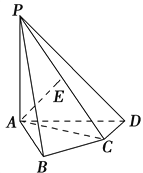
【题目】如图，在三棱柱
中，
面
，
，
，
，
是棱
上一点．
（1）求证：
；
（2）若
分别为、
的中点，求证：
//平面
．
【答案】（1）见解析（2）见解析
【解析】
（1）根据勾股定理得BC⊥AC，再根据线面垂直判定与性质定理得结果，（2）根据平行四边形性质得线线平行，再根据线面平行判定定理得结果.
证明：（Ⅰ）因为三棱柱ABC-A1B1C1中CC1⊥平面ABC，
所以CC1⊥BC．
因为AC=BC=2，
，
所以由勾股定理的逆定理知BC⊥AC．
又因为AC∩CC1=C，
所以BC⊥平面ACC1A1．
因为AM
平面ACC1A1，
所以BC⊥AM．
(Ⅱ）过N作NP∥BB1交AB1于P，连结MP ，则NP∥CC1．
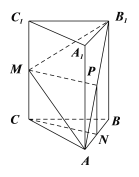
因为M,N分别为CC1, AB中点，
所以 
，
．
因为 BB1=CC1，所以 NP=CM．
所以 四边形MCNP是平行四边形．所以 CN//MP．
因为 CN
平面AB1M，MP平面AB1M，
所以 CN //平面AB1M．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
