Question

【题目】下列四个命题：

①圆与直线相交，所得弦长为；

②直线与圆恒有公共点；

③若棱长为的正方体的顶点都在同一球面上，则该球的表面积为；

④若棱长为的正四面体的顶点都在同一球面上，则该球的体积为.

其中，正确命题的序号为__________．（写出所有正确命题的序号）

Answer 1

【答案】②④.

【解析】试题分析：①②是直线和圆的位置关系及弦长问题，一般转化为圆心到直线的距离问题，但本题中很容易看出①中直线x﹣2y=0过圆心，②中直线和圆均过原点；③④为与球有关的组合体问题，结合球的截面性质，球心与截面圆心的连线垂直于截面圆处理．

详解：①圆心（﹣2，﹣1）在直线x﹣2y=0上，即直线x﹣2y=0过圆心，所得弦长为直径4，结论错误；

②∵直线y=kx与圆（x﹣cosθ）2+（y﹣sinθ）2=1横过原点，故恒有公共点正确；

③球直径为正方体的对角线长即 ，故求半径R= ，球表面积为s=4πR2=27π，结论错误；

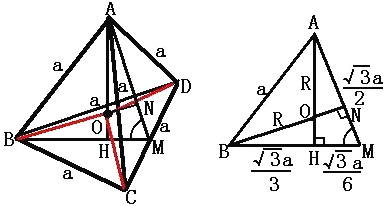
由上图可知，AH=， ，∴R=，

∵，∴，∴ ，结论正确．

故答案为：②④