题目内容
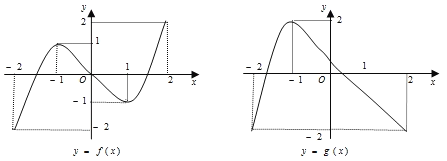
【题目】定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x<0时,f(x)>0恒成立,且nf(x)=f(nx).(n是一个给定的正整数).
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-2,5]上总有f(x)≤10成立,试确定f(1)应满足的条件;
(3)当a<0时,解关于x的不等式![]() .
.
【答案】(1)见解析;(2)f(1)![]() [-5,0);(3)见解析
[-5,0);(3)见解析
【解析】
(1)利用函数奇偶性的定义,结合抽象函数关系,利用赋值法进行证明
(2)结合函数单调性的定义以及最值函数成立问题进行证明即可
(3)利用抽象函数关系,结合函数奇偶性和单调性定义转化为一元二次不等式,讨论参数的范围进行求解即可
(1)f(x)为奇函数,证明如下;
由已知对于任意实数x,y都有f(x+y)=f(x)+f(y)恒成立.
令x=y=0,得f(0+0)=f(0)+f(0),所以f(0)=0.
令y=-x,得f(x-x)=f(x)+f(-x)=0.
所以对于任意x,都有f(-x)=-f(x).
所以f(x)是奇函数.
(2)设任意x1,x2且x1<x2,则x2-x1>0,由已知f(x2-x1)<0,
又f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1)<0,得f(x2)<f(x1),
根据函数单调性的定义和奇函数的性质知f(x)在(-∞,+∞)上是减函数.
所以f(x)在[-2,5]上的最大值为f(-2).
要使f(x)≤10恒成立,当且仅当f(-2)≤10,
又因为f(-2)=-f(2)=-f(1+1)=-2f(1),所以f(1)≥-5.
又x>1,f(x)<0,所以f(1)∈[-5,0).
(3)∵![]() .,
.,
∴f(ax2)-f(a2x)>n2[f(x)-f(a)].
所以f(ax2-a2x)>n2f(x-a),
所以f(ax2-a2x)>f[n2(x-a)],
因为f(x)在(-∞,+∞)上是减函数,
所以ax2-a2x<n2(x-a).
即(x-a)(ax-n2)<0,
因为a<0,所以(x-a)(x![]() )>0.
)>0.
讨论:
①当a<![]() <0,即a<-n时,原不等式的解集为{x|x>
<0,即a<-n时,原不等式的解集为{x|x>![]() 或x<a};
或x<a};
②当a=![]() ,即a=-n时,原不等式的解集为{x|x≠-n};
,即a=-n时,原不等式的解集为{x|x≠-n};
③当![]() <a<0,即-n<a<0
<a<0,即-n<a<0![]() }.
}.

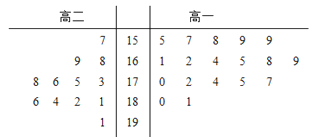
【题目】下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届
获得的金牌数的统计数据:
年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
主办国家 | 联邦 德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大 利亚 | 希腊 | 中国 |
上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,
(1)求出主办国在上届所获金牌数(设为![]() )与在当届所获金牌数(设为
)与在当届所获金牌数(设为![]() )之间的线性回归方程
)之间的线性回归方程
![]() 其中
其中![]()
(2)在2008年第29届北京奥运会上日本获得9块金牌,则据此线性回归方程估计在2020 年第 32 届东
京奥运会上日本将获得的金牌数为(所有金牌数精确到整数)