题目内容
【题目】已知圆C:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 被圆C截得的弦长为
被圆C截得的弦长为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当t =1时,由直线![]() 上的动点P引圆C的两条切线,若切点分别为A,B,则直线AB是否恒过一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
上的动点P引圆C的两条切线,若切点分别为A,B,则直线AB是否恒过一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
【答案】(1)t =11;(2)![]()
【解析】
(1)根据垂径定理列式求实数![]() 的值;(2)先根据切点A,B在以CP为直径的圆,再根据两圆方程得切点弦方程,最后根据动点P在直线
的值;(2)先根据切点A,B在以CP为直径的圆,再根据两圆方程得切点弦方程,最后根据动点P在直线![]() 上,确定切点弦过定点.
上,确定切点弦过定点.
(1)圆C的方程可化为 ![]() ,
,
则圆心C到直线![]() 的距离为
的距离为 ![]()
又弦长为![]() ,则
,则 ![]()
即![]() ,解得t =11.
,解得t =11.
(2)当t =1时,圆C的方程为![]() ①
①
则圆心为C(3,5),半径![]() ,圆C与直线
,圆C与直线![]() 相离
相离
假设在直线AB上存在一个定点满足条件,设动点P(m,n),由已知得PA⊥AC,PB⊥BC
则A,B在以CP为直径的圆(x﹣3)(x﹣m)+(y﹣5)(y﹣n)=0
即![]() ②
②
①﹣②得,直线AB的方程为(m﹣3)x+(n﹣5)y﹣3m﹣5n﹣6=0③
又点P(m,n)在直线![]() 上,则m+3n+12=0,即m=﹣3n﹣12,代入③式
上,则m+3n+12=0,即m=﹣3n﹣12,代入③式
得(﹣3n﹣15)x+(n﹣5)y+4n+30=0
即直线AB的方程为15x+5y﹣30+n(3x﹣y﹣4)=0
因为上式对任意n都成立,故![]() ,得
,得 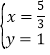
故直线AB恒过一个定点,定点坐标为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







