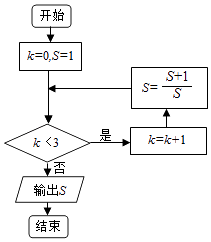
��Ŀ����
����Ŀ��ij��ҵ��Ƹ��ѧ��ҵ���������ۺϲ��ԣ�¼����14��Ů����6����������20��ѧ���IJ��Գɼ��羥Ҷͼ��ʾ(��λ����)���dzɼ���С��80����Ϊ![]() �ȣ�С��80����Ϊ
�ȣ�С��80����Ϊ![]() �ȣ�
�ȣ�

(1)��Ů���ɼ�����λ���������ɼ���ƽ������
(2)����÷ֲ�����ķ�����![]() �Ⱥ�
�Ⱥ�![]() ���й���ȡ5����ɡ������Ŷӡ������
���й���ȡ5����ɡ������Ŷӡ������![]() �Ⱥ�
�Ⱥ�![]() ���зֱ�鼸�ˣ�
���зֱ�鼸�ˣ�
(3)��(2)�ʵĻ����ϣ��ִӸá������Ŷӡ��������ȡ2�ˣ���������1����![]() �ȵĸ��ʣ�
�ȵĸ��ʣ�
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
����������������1���ɾ�Ҷͼ�ɵ�Ů���ɼ�����λ��Ϊ![]() ��������ƽ���ɼ�Ϊ
��������ƽ���ɼ�Ϊ![]() ��
��
��2���÷ֲ�����ɵ�![]() �ֱ��ȡ������Ϊ
�ֱ��ȡ������Ϊ![]() �ˡ�
�ˡ�![]() �ˣ��ֱ��Ϊ
�ˣ��ֱ��Ϊ![]() ��
��![]() ���оٿɵ��ܵĻ����¼�����
���оٿɵ��ܵĻ����¼�����![]() ��������������
��������������![]() ����
����![]() ����7�����ɸ��ʹ�ʽ���������
����7�����ɸ��ʹ�ʽ���������
��⣺(1)�����о�Ҷͼ֪��Ů���ɼ�����λ����75.5.
�����ɼ���ƽ��ֵΪ![]() ��
��![]() (69��76��78��85��87��91)��81.
(69��76��78��85��87��91)��81.
(2)�÷ֲ�����ķ�����A�Ⱥ�B��ѧ���й���ȡ5�ˣ�ÿ���˱����еĸ�����![]() .
.
���ݾ�Ҷͼ֪��A����8�ˣ�B����12�ˣ�
���Գ�ȡ��A����8��![]() ��2(��)��B����12��
��2(��)��B����12��![]() ��3(��)
��3(��)
(3)�dz�ȡ��A��2�˷ֱ�ΪA1��A2����ȡ��B��3�˷ֱ�ΪB1��B2��B3������5���г�ȡ2�˵����п��ܵĽ��Ϊ(A1��A2)��(A1��B1)��(A1��B2)��(A1��B3)��(A2��B1)��(A2��B2)��(A2��B3)��(B1��B2)��(B1��B3)��(B2��B3)��10�֣�
����������1����A�ȵĽ��Ϊ(A1��A2)��(A1��B1)��(A1��B2)��(A2��B3)��(A2��B1)��(A2��B2)��(A2��B3)��7�֣�
����������1����A�ȵĸ���Ϊ![]() .
.