题目内容
【题目】已知公差不为零的等差数列{an}中， S2＝16，且
成等比数列.
（1）求数列{an}的通项公式；
（2）求数列{|an|}的前n项和Tn.
【答案】（1）an＝11－2n(n∈N*)．（2）见解析．
【解析】
(1)S2＝16，
成等比数列，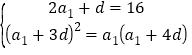
解得首项和公差进而得到通项；（2）当n≤5时，Tn＝a1＋a2＋…＋an, 直接按照等差数列求和公式求和即可, n≥6,Tn＝a1＋a2＋…＋a5－a6－a7－ …－an =n2－10n＋50,写成分段即可.
（1）由S2＝16，成等比数列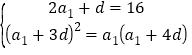，得解得
所以等差数列{an}的通项公式为an＝11－2n(n∈N*)．
（2）当n≤5时，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋an＝Sn＝－n2＋10n.
当n≥6时，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋a5－a6－a7－ …－an＝2S5－Sn＝2×(－52＋10×5)－(－n2＋10n)＝n2－10n＋50，
故Tn＝
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
转速 | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数 | 5 | 7 | 8 | 9 | 11 |
（1）如果
对
有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有1个，那么机器的运转速度应控制在什么范围内？参考公式：
，
．
【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系，在高中生中随机地抽取了90名学生调查，得到了如下列联表：
喜欢数学 | 不喜欢数学 | 总计 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
总计 | ③ | ④ | 90 |
（1）求①②③④处分别对应的值；
（2）能有多大把握认为“高中生的性别与喜欢数学”有关？
附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
.
