题目内容
已知抛物线y2=4x的准线与双曲线
-y2=1(a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则a的值为( )
| x2 |
| a2 |
A.
| B.
| C.
| D.
|
∵抛物线的方程为y2=4x,
∴抛物线的准线为x=-1,焦点为F(1,0).
又∵直线x=-1交双曲线
-y2=1于A、B两点,△FAB为直角三角形.
∴△FAB是等腰直角三角形,AB边上的高FF'=2
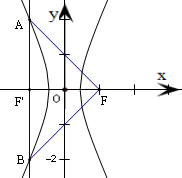
由此可得A(-1,2)、B(-1,-2),如图所示
将点A或点B的坐标代入双曲线方程,得
-4=1,解之得a=
(舍负)
故选:D
∴抛物线的准线为x=-1,焦点为F(1,0).
又∵直线x=-1交双曲线
| x2 |
| a2 |
∴△FAB是等腰直角三角形,AB边上的高FF'=2
由此可得A(-1,2)、B(-1,-2),如图所示
将点A或点B的坐标代入双曲线方程,得
| 1 |
| a2 |
| ||
| 5 |
故选:D


练习册系列答案
相关题目