题目内容
已知抛物线C:y2=-2px(p>0)上横坐标为-3的一点到准线的距离为4.
(1)求p的值;
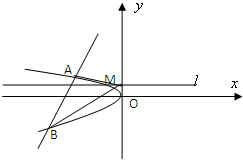
(2)设动直线y=x+b与抛物线C相交于A、B两点,问在直线l:y=2上是否存在与b的取值无关的定点M,使得∠AMB被直线l平分?若存在,求出点M的坐标;若不存在,说明理由.
(1)求p的值;
(2)设动直线y=x+b与抛物线C相交于A、B两点,问在直线l:y=2上是否存在与b的取值无关的定点M,使得∠AMB被直线l平分?若存在,求出点M的坐标;若不存在,说明理由.

(1)由已知得|-3-
|=4,∵p>0,∴p=2
(2)令A(x1,y1),B(x2,y2),设存在点M(a,2)满足条件,由已知得kAM=-KBM,
即有
+
=0,x1=-
,x2=-
;
整理得y1y2(y1+y2)+4a(y1+y2)-2(y12+y22)-16a=0;
由
,得 y2+4y-4b=0,即 y1+y2=-4,y1y2=-4b,
有-4b•(-4)+4a(-4)-2[(-4)2+8b]-16a=0,∴a=-1,
因此存在点M(-1,2)满足题意.
| p |
| 2 |
(2)令A(x1,y1),B(x2,y2),设存在点M(a,2)满足条件,由已知得kAM=-KBM,
即有
| y1-2 |
| x1-a |
| y2-2 |
| x2-a |
| y12 |
| 4 |
| y22 |
| 4 |
整理得y1y2(y1+y2)+4a(y1+y2)-2(y12+y22)-16a=0;
由
|
有-4b•(-4)+4a(-4)-2[(-4)2+8b]-16a=0,∴a=-1,
因此存在点M(-1,2)满足题意.

练习册系列答案
相关题目