题目内容
【题目】一房产商竞标得一块扇形![]() 地皮,其圆心角
地皮,其圆心角![]()
![]() ,半径为
,半径为![]()
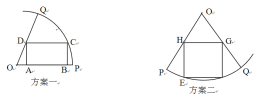
![]() ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形![]() 的一边
的一边![]() 在半径
在半径![]() 上,
上,![]() 在圆弧上,
在圆弧上,![]() 在半径
在半径![]() ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点![]() 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。
【答案】见解析
【解析】
试题分析:由题为三角函数的应用问题,结合题中条件及两个方案(面积大者为好方案),需先设出![]() 再分别表示出矩形的长和宽,建立面积关于
再分别表示出矩形的长和宽,建立面积关于![]() 的函数利用三角函数的性质可求出最值,分别比较两种方案的最值可确定最优方案。
的函数利用三角函数的性质可求出最值,分别比较两种方案的最值可确定最优方案。
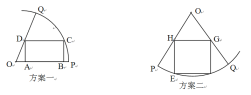
试题解析:如图,连![]() ,设
,设![]() ,在
,在![]() 中,
中,![]() ,则
,则![]() 在
在![]() 中,
中,![]() :按方案一,得
:按方案一,得![]() ,则
,则![]() ,设矩形
,设矩形![]() 的面积为
的面积为![]() ,则
,则
由![]() 得
得![]() 。所以当
。所以当![]() ,即
,即![]() 时
时![]() 。
。
按方案二:如图作![]() 的平分线分别交
的平分线分别交![]() 于点
于点![]() ,连
,连![]() 。设
。设![]() ,在
,在![]() 中,
中,![]() 在
在![]() 中,
中,![]() ,得
,得![]() ,则
,则![]() ,设矩形
,设矩形![]() 的面积为
的面积为![]() ,则
,则![]()
![]() ,由
,由![]() ,则
,则![]() ,所以当
,所以当![]() ,即
,即![]() 时
时![]() 。
。
![]() ,即
,即![]() 。
。
答:给房产商提出决策建议:选用方案一更好。

练习册系列答案
相关题目
【题目】在英语中不同字母出现的频率彼此不同且相差很大,但同一个字母的使用频率相当稳定,有人统计了40多万个单词中5个元音字母的使用频率,结果如下表所示:
元音字母 | A | E | I | O | U |
频率 | 7.88% | 12.68% | 7.07% | 7.76% | 2.80% |
(1)从一本英文(小说类)书里随机选一页,统计在这一页里元音字母出现的频率;
(2)将你统计得出的频率与上表中的频率进行比较,结果是否比较接近?你认为存在差异的原因是什么.