题目内容
【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则把
,则把![]() 叫闭函数。
叫闭函数。
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)已知![]() 是正整数,且定义在
是正整数,且定义在![]() 的函数
的函数![]() 是闭函数,求正整数
是闭函数,求正整数![]() 的最小值,及此时实数k的取值范围。
的最小值,及此时实数k的取值范围。
【答案】(1)![]() ;(2)不是,理由见解析;(3)
;(2)不是,理由见解析;(3)![]() 。
。
【解析】
试题分析:(1)由题意,![]() 在
在![]() 上递减,在
上递减,在![]() 上的值域为
上的值域为![]() ,故有
,故有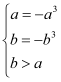 ,求得
,求得![]() 、
、![]() 的值,可得结论;(2)取
的值,可得结论;(2)取![]() ,则由
,则由![]() ,可得
,可得![]() 不是
不是![]() 上的减函数。同理求得
上的减函数。同理求得![]() 不是
不是![]() 上的增函数,从而该函数不是闭函数;(3)由题意,可得方程
上的增函数,从而该函数不是闭函数;(3)由题意,可得方程![]() 在
在![]() 上有两个不等的实根.利用基本不等式求得当
上有两个不等的实根.利用基本不等式求得当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .再根据函数
.再根据函数![]() 在
在![]() 上递减,在
上递减,在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点,可得正整数
有两个交点,可得正整数![]() 的最小值为
的最小值为![]() ,此时,
,此时,![]() ,由此求得
,由此求得![]() 的范围。
的范围。
试题解析:(1)由题意,![]() 在
在![]() 上递减,则
上递减,则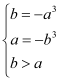 解得
解得![]() 所以,所求的区间为
所以,所求的区间为![]() 。
。
(2)取![]() 则
则![]() ,即
,即![]() 不是
不是![]() 上的减函数。取
上的减函数。取![]()
![]() ,即
,即![]() 不是
不是![]() 上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)![]() 是闭函数,则存在区间
是闭函数,则存在区间![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ,
,![]() 在
在![]() 单调递增,即
单调递增,即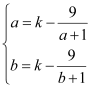 ,
,![]() 为方程
为方程![]() 的两个实根,即方程
的两个实根,即方程![]() 在
在![]() 上有两个不等的实根。
上有两个不等的实根。![]() ,当且仅当
,当且仅当![]() 时取等号考察函数
时取等号考察函数![]()
∵函数![]() 在
在![]() 上递减,∴
上递减,∴![]() 。
。
∵![]() 在
在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点。
有两个交点。
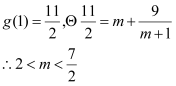
所以正整数![]() 的最小值为
的最小值为![]() ,
,![]() ,此时
,此时![]() 的取值范围为
的取值范围为![]() 。
。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目