题目内容
已知函数f(x)=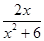 .
.
(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
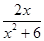 .
.(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
(1)-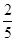 (2)
(2)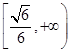
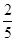 (2)
(2)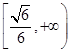
(1)f(x)>k?kx2-2x+6k<0.
由已知{x|x<-3,或x>-2}是其解集,得kx2-2x+6k=0的两根是-3,-2.
由根与系数的关系可知(-2)+(-3)=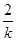 ,即k=-
,即k=-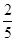
(2)∵x>0,f(x)=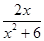 =
=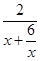 ≤
≤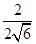 =
=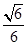 ,当且仅当x=
,当且仅当x=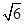 时取等号.由已知f(x)≤t对任意x>0恒成立,故t≥
时取等号.由已知f(x)≤t对任意x>0恒成立,故t≥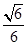 ,即t的取值范围是
,即t的取值范围是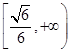 .
.
由已知{x|x<-3,或x>-2}是其解集,得kx2-2x+6k=0的两根是-3,-2.
由根与系数的关系可知(-2)+(-3)=
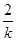 ,即k=-
,即k=-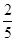
(2)∵x>0,f(x)=
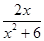 =
=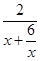 ≤
≤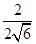 =
=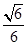 ,当且仅当x=
,当且仅当x=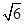 时取等号.由已知f(x)≤t对任意x>0恒成立,故t≥
时取等号.由已知f(x)≤t对任意x>0恒成立,故t≥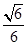 ,即t的取值范围是
,即t的取值范围是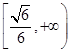 .
.
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
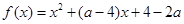 .
.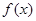 是偶函数,求实数
是偶函数,求实数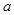 的值;
的值;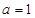 时,求
时,求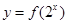 在区间
在区间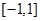 上的值域.
上的值域.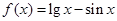 ,则
,则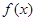 在
在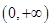 上的零点个数为( )
上的零点个数为( )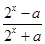 在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)
在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)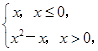 若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( ) 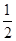 ,1
,1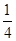 ,0
,0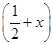 =f
=f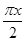 ;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).