题目内容
若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间 ( ).
| A.(a,b)和(b,c)内 | B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(-∞,a)和(c,+∞)内 |
A
由于a<b<c,所以f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0.因此有f(a)·f(b)<0,f(b)·f(c)<0,又因f(x)是关于x的二次函数,函数的图象是连续不断的曲线,因此函数f(x)的两零点分别位于区间(a,b)和(b,c)内,故选A.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
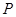 和
和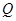 (万元),它们与投入资金
(万元),它们与投入资金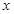 (万元)的关系依次是:其中
(万元)的关系依次是:其中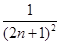 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<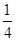 .
. ,则当x∈(-∞,-2)时,f(x)的解析式为( )
,则当x∈(-∞,-2)时,f(x)的解析式为( )

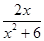 .
. 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称. 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.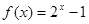 ,
,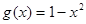 ,规定:当
,规定:当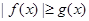 时,
时, 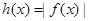 ;当
;当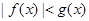 时,
时,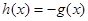 ,则
,则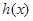 ( )
( )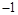 ,最大值1
,最大值1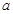 元,每期利率为
元,每期利率为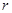 ,设本利和为
,设本利和为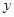 ,存期为
,存期为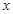 ,则
,则