Question

【题目】已知函数 .

（1）若在 处导数相等，证明： ；

（2）若对于任意 ，直线 与曲线都有唯一公共点，求实数的取值范围.

Answer 1

【答案】（I）见解析（II）

【解析】

（1）由题x＞0，，由f（x）在x=x1，x2（x1≠x2）处导数相等，得到，得，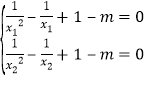

由韦达定理得，由基本不等式得，得，由题意得，令,则，令，，利用导数性质能证明．

（2）由得，令，

利用反证法可证明证明恒成立。

由对任意，只有一个解，得为上的递增函数，得，令，由此可求的取值范围..

（I）

令，得，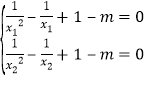

由韦达定理得

即，得

令,则，令，

则，得

（II）由得

令，

则，，

下面先证明恒成立。

若存在，使得，，，且当自变量充分大时，，所以存在，，使得，，取，则与至少有两个交点，矛盾。

由对任意，只有一个解，得为上的递增函数，

得，令，则，

得