题目内容
【题目】已知矩形纸片![]() 中,
中,![]() ,将矩形纸片的右下角沿线段
,将矩形纸片的右下角沿线段![]() 折叠,使矩形的顶点B落在矩形的边
折叠,使矩形的顶点B落在矩形的边![]() 上,记该点为E,且折痕
上,记该点为E,且折痕![]() 的两端点M,N分别在边
的两端点M,N分别在边![]() 上.设
上.设![]() ,
,![]() 的面积为S.
的面积为S.
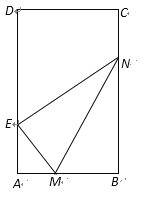
(1)将l表示成θ的函数,并确定θ的取值范围;
(2)求l的最小值及此时![]() 的值;
的值;
(3)问当θ为何值时,![]() 的面积S取得最小值?并求出这个最小值.
的面积S取得最小值?并求出这个最小值.
【答案】(1)![]() (2)
(2)![]() ,
,![]() 的最小值为
的最小值为![]() .(3)
.(3)![]() 时,面积
时,面积![]() 取最小值为
取最小值为![]()
【解析】
(1)![]() ,利用三角函数定义分别表示
,利用三角函数定义分别表示![]() ,且
,且![]() ,即可得到
,即可得到![]() 关于
关于![]() 的解析式;
的解析式;![]() ,
,![]() ,则
,则 ,即可得到
,即可得到![]() 的范围;
的范围;
(2)由(1),若求l的最小值即求![]() 的最大值,即可求
的最大值,即可求![]() 的最大值,设为
的最大值,设为![]() ,令
,令![]() ,则
,则![]() ,即可设
,即可设![]() ,利用导函数判断函数的单调性,即可求得
,利用导函数判断函数的单调性,即可求得![]() 的最大值,进而求解;
的最大值,进而求解;
(3)由题,![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,利用导函数求得
,利用导函数求得![]() 的最大值,即可求得
的最大值,即可求得![]() 的最小值.
的最小值.
解:(1)![]() ,
,
故![]() .
.
因为![]() ,所以
,所以![]() ,,
,,
所以![]() ,
,
又![]() ,
,![]() ,则
,则 ,所以
,所以![]() ,
,
所以![]()
(2)记![]() ,
,
则![]() ,
,
设![]() ,
,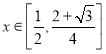 ,则
,则![]() ,
,
记![]() ,则
,则![]() ,
,
令![]() ,则
,则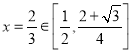 ,
,
当![]() 时,
时,![]() ;当
;当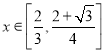 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在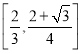 上单调递减,
上单调递减,
故当![]() 时
时![]() 取最小值,此时
取最小值,此时![]() ,
,![]() 的最小值为
的最小值为![]() .
.
(3)![]() 的面积
的面积![]() ,
,
所以![]() ,设
,设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() ,
, ,
,
所以当![]() 时,
时,![]() ;当
;当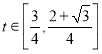 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在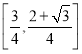 上单调递减,
上单调递减,
故当![]() ,即
,即![]() 时,面积
时,面积![]() 取最小值为
取最小值为![]()

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目