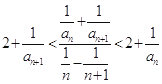题目内容
【题目】观察下列各不等式:![]() ,
,![]() ,
,![]() ,
,![]()
…
(1)由上述不等式,归纳出一个与正整数![]() 有关的一般性结论;
有关的一般性结论;
(2)用数学归纳法证明你得到的结论.
【答案】
(1)
【解答】解:观察上述各不等式,得到与正整数n有关的一般不等式为
![]() 且
且![]() .
.
(2)
【解答】
以下用数学归纳法证明这个不等式.
证明:①当n=2时,由题设可知,不等式显然成立.
②假设当n=k时,不等式成立,即![]() ,
,
那么,当n=k+1时,有![]()
![]()
![]()
![]()
![]() .
.
所以当n=k+1时,不等式也成立.
根据①和②,可知不等式对任何![]() 且
且 ![]() 都成立.
都成立.
【解析】本题主要考查了数学归纳法证明不等式,解决问题的关键是根据1)由上述不等式,归纳出表达式的左侧的关系与右侧分子与分母的特征写出一个正整数 ![]() ,
, ![]() 有关的一般性结论;(2)利用数学归纳法证明步骤,直接证明即可.
有关的一般性结论;(2)利用数学归纳法证明步骤,直接证明即可.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
【题目】某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35至50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(Ⅰ)用分层抽样的方法在35至50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有l人的学历为研究生的概率;
(Ⅱ)在该校教师中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取l人,此人的年龄为50岁以上的概率为 ![]() ,求x、y的值.
,求x、y的值.