题目内容
【题目】已知数列 ![]() 的各项均为正整数,对于任意n∈N* , 都有
的各项均为正整数,对于任意n∈N* , 都有 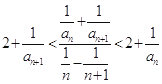 成立,且
成立,且 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)猜想数列 ![]() 的通项公式,并给出证明.
的通项公式,并给出证明.
【答案】
(1)
解:因为 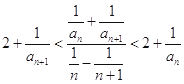 ,
, ![]()
当 ![]() 时,由
时,由 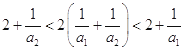 ,即有
,即有 ![]() ,
,
解得 ![]() .因为
.因为 ![]() 为正整数,故
为正整数,故 ![]() .
.
当 ![]() 时,由
时,由 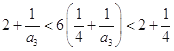 ,
,
解得 ![]() ,所以
,所以 ![]() .
.
(2)
解:由 ![]() ,
, ![]() ,
, ![]() ,猜想:
,猜想: ![]()
下面用数学归纳法证明.
①当 ![]() ,
, ![]() ,
, ![]() 时,由(1)知
时,由(1)知 ![]() 均成立.
均成立.
②假设 ![]() 成立,则
成立,则 ![]() ,
,
由条件得 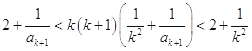 ,
,
所以 ![]() ,
,
所以 ![]()
因为 ![]() ,
, ![]() ,
, ![]() ,
,
又 ![]() ,所以
,所以 ![]() .
.
即 ![]() 时,
时, ![]() 也成立.
也成立.
由①,②知,对任意 ![]() ,
, ![]() .
.
【解析】本题主要考查了数学归纳法证明不等式,解决问题的关键是根据(1)先列出 ![]() 所满足条件
所满足条件 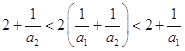 ,化简得
,化简得 ![]() ,再根据数列
,再根据数列 ![]() 的各项均为正整数这一限制条件求出
的各项均为正整数这一限制条件求出 ![]() ,同理可得
,同理可得 ![]() (2)猜想:
(2)猜想: ![]() ,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得
,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得 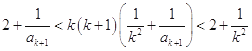 ,所以
,所以 ![]() ,所以
,所以 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,所以
,所以 ![]()

练习册系列答案
相关题目

