题目内容
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 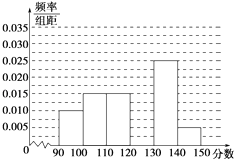
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
【答案】
(1)解:分数在[120,130)内的频率为:
1﹣(0.01+0.015+0.025+0.005)×10=0.3,
∴数学分数恰在[120,130)内的频率为0.3.
(2)解:由频率分布直方图估计本次考试的中位数为:
![]() =
= ![]() .
.
(3)解:由题意[110,120)分数段的人数为60×0.15=9人,
在[120,130)分数段的人数为60×0.3=18人,
∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,
∴需在[110,120)分数段内抽取两人,并分别记为m,n,
在[120,130)分数段内抽取4 人,并分别记为a,b,c,d,
设“从样本中任取2人,至多有1人在分数在[120,130)内”为事件A,
则基本事件共有:n= ![]() 个,
个,
则事件A包含的基本事件个数m=15﹣ ![]() =9个,
=9个,
∴至多有1人在分数段[120,130)内的概率P(A)= ![]() =
= ![]() .
.
【解析】(1)利用频率分布直方图能求出分数在[120,130)内的频率.(2)由频率分布直方图能估计本次考试的中位数.(3)[110,120)分数段的人数为9人,在[120,130)分数段的人数为18人,用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,需在[110,120)分数段内抽取两人,在[120,130)分数段内抽取4 人,由此能求出至多有1人在分数段[120,130)内的概率.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.