题目内容
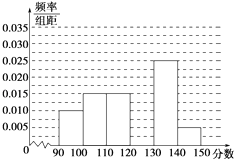
【题目】某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图. 
(1)若该校高一年级共有学生1000人,试估计成绩不低于60分的人数;
(2)为了帮助学生提高数学成绩,学校决定在随机抽取的50名学生中成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙恰好被安排在同一小组的概率.
【答案】
(1)解:根据频率分布直方图,
成绩不低于6(0分)的频率为1﹣10×(0.004+0.010)=0.86.
由于该校高一年级共有学生1000人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于6(0分)的人数为1000×0.86=860人.
(2)解:成绩在[40,50)分数段内的人数为50×0.04=2人
成绩在[90,100]分数段内的人数为50×0.1=5人
[40,50)内有2人,记为甲、A.
[90,100)内有5人,记为乙、B、C、D、E.
则“二帮一”小组有以下20种分组办法:甲乙B,甲乙C,甲乙D,甲乙E,甲BC,
甲BD,甲BE,甲CD,甲CE,甲DE,A乙B,A乙C,A乙D,A乙E,ABC,ABD,ABE,ACD,ACE,ADE
其中甲、乙两同学被分在同一小组有4种办法:甲乙B,甲乙C,甲乙D,甲乙E
所以甲乙两同学恰好被安排在同一小组的概率为 ![]()
【解析】(1)根据频率分布直方图,成绩不低于60分的频率,然后根据频数=频率×总数可求出所求;(2)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.